Introduction to Floating Point Number

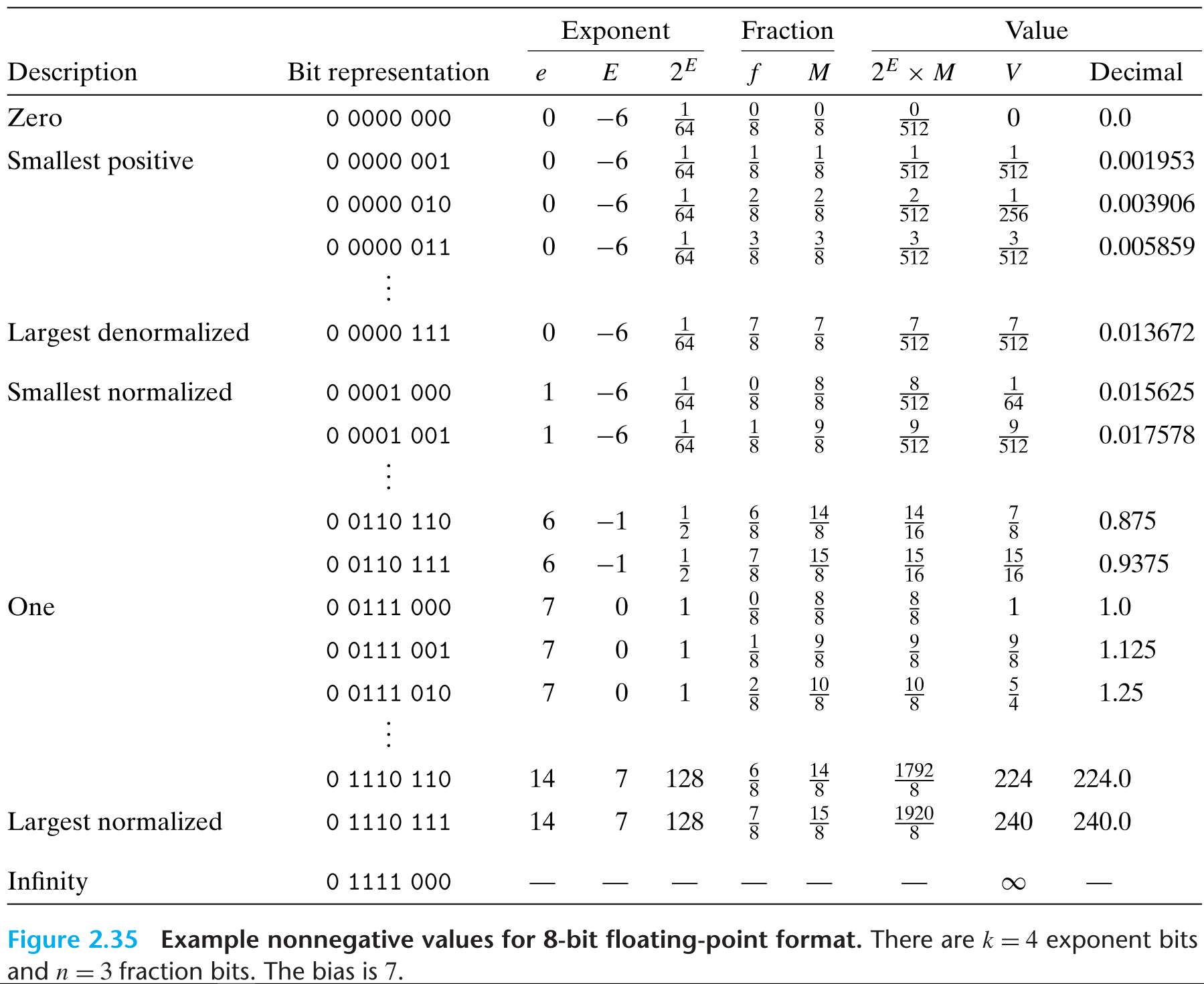
整数

在讲浮点数在二进制的表示之前，我们要先了解整数在二进制中的表述。

其实和十进制一样，只不过在十进制中，每位数的权是 $10^i$ (where i is the index starting from 0) 那么在二进制中则是以 $2^i$ 作为权。

最常见的整数即为 int32 ，长度为 4 bytes， 32 bits，但其中最高位为 sign bit ， 带有 $-2^{31}$ 的权（例：100...000 共 32 bit，值为 -2^31 = -2,147,483,648 ）。由此看来，最高位还兼有表示正负的功能（最高位是 1 为负，0 为正），而其余位照常表示正权值，也就是说，INT_MIN = 100...000 = -2^31

但这样会带来一个问题，0 这个数，在二进制中应表示为 000...000 ，那就说明 0 在此处被看做了一个正数，由对称性得， INT_MAX = 011...111 = 2,147,483,647 ，或者在数学上 ${\sum }_{i=0}^{30}{2}^i$

浮点数

那要表示 小数 ，也就是浮点数，最显而易见的做法就是仿照十进制的做法，取 16 bit 表示小数点前面部分（characteristic），权为 $[2^0,2^{15}]$ ；取 16 bit 表示小数点后面部分（mantissa），权为 $[2^{-1},2^{-16}$]。

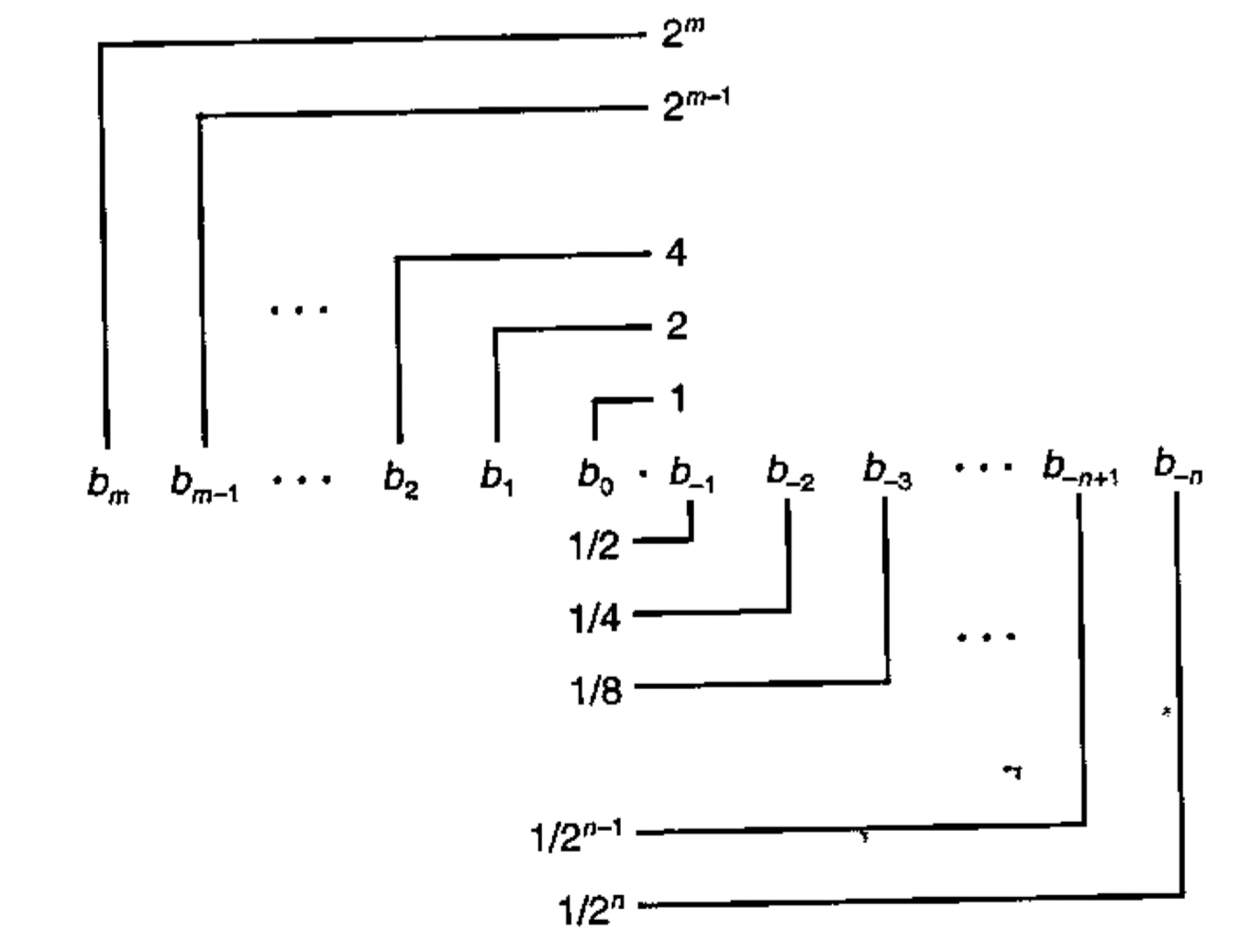
显然，这样会带来严重的空间浪费，所以，计算机科学家们设计了一种巧妙的做法，能用 32 bit 表示 $\pm 10^{-38}$ to $10^{38}$ 的范围 (1.2E-38 to 3.4E+38)，但是代价是存在误差，比如著名的 0.1 + 0.2 = 0.30000000000000004 （Floating Point Math）

根据 bit 的排列不同，共有四种形式，一一介绍

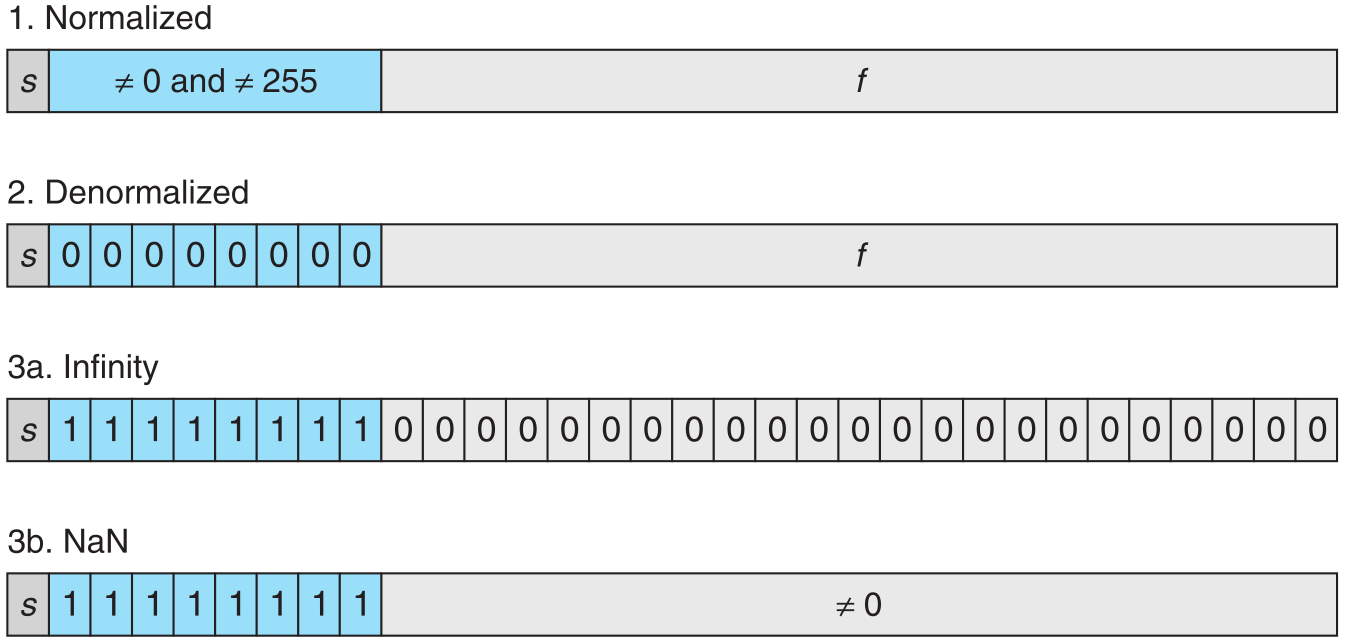
General

先不纠结数值，先看 bit 的排列，分为三组，符号位 (sign bit)，指数部分 (exponent bits)，和有效部分 (significant bits / fraction bits)。

整体思想是，符号位 S 为 1 表示负数， 0 表示正数，由指数部分算出 E ，由有效部分算出 M 。 最终结果可以表示为

$(-1{)}^S\times 2^E\times M$

看出点什么了吗，本质上是科学计数法呀！

我们在十进制中表示为 $1.23\times 10^e$ ，自然也能在二进制中表示 $1.01\times 2^e$ ， 这其中的 $e$ ，便是通过 8 exponent bits 表示的。

而我们要表示小数，$E$ 自然也要有正有负（负的情况才有小数呀），而此时的 exponent bits 可是没有符号的（最高位的符号是整个数的符号，而不是 exponent 的符号），所以最直接想到的就是像 int 一样减去一半，这样就有正有负了。此时 exponent bits 表示的范围从 $[255,0]$ → $[128,-127]$ 。 此时我们不是像 int 一样最高位置为符号位，而是像 uint 一样 literally 的读取它，再做减法。

我们把这个要减去的数叫做 bias ，它的数值为 $2^{k-1}-1$ (其中 k 为 exponent bits 位数，8 for float32 and 16 for double64, 即 127 for float32 and 1023 for double64) 。

此时又有特殊的地方，当值为 128（即 exponent bits 全为 1 时）和值为 -127 （exponent bits 全为 0 时），被设定为了特殊值（见上图的 2 和 3），需要特殊处理，去掉这两个值后，现在它所能表示的大体范围就变成 $[2^{127},2^{-126}]$ 了。 现在我们取 exponent bits 的结果为 $e$ ，公式中的 $E$ 可看作 $E=e-Bias$

说大体范围是因为具体数值是由 fraction 部分确定的，在十进制中，取前面表示数值部分为 $n$， $n$ 的选取规则是 $n\ge 1$ 且 $n<10$ ，那么在二进制中，我们选取 $n\ge 1$ 且 $n<2$ …??? wait a second!

在二进制中，只有一个数满足这个条件，那就是 1 。所以小数点前面是确定的，是 $1.x$ ，x 的值由正常二进制小数组成。也就是说，significant bits/fraction bits 全部当作小数点右边的数正常计算即可（每位权值为 $[2^{-1},2^{-23}]$），把这个小数叫做 $f$ ，最后 $f+1$ 即可正确表示。

Case 1: Denormalized Values

• 出现情况

  • exponent bits 全为 0

• $E=1-Bias$

  • 为什么是 1 - Bias？不是 $e-Bias$ ，即 $0-Bias$ ?
    • 现在的 exponent bits 全为 0，对于下一个数，如果当 exponent bits 不全为 0 ，那就是从 1 开始喽，所以就是 1 - Bias 喽，主要为了更平滑地从此处的 Denormalized 过渡到之后的 Normalized。

• $M=f$

  • 为什么不 + 1 ？
    • 用于表示非常接近 0 的数。
    • 如果 + 1， 0 要怎么表示呢？
      • 实际上有两个零，+0.0, -0.0，区别只是 sign bit 不同

• 最终结果 V： $V=(-1{)}^S\times 2^E\times M$

Case 2: Normalized Values

• 出现情况

  • exponent bits 不全为 0 且不全为 1

• $E=e-Bias$

• $M=1+f$

• 最终结果 V： $V=(-1{)}^S\times 2^E\times M$

这下是不是就很 Normal 了？

Case 3: Special Values

• When the exponent field is all ones
  • When the fraction field is all zeros, the resulting values represent infinity
  • When the fraction field is nonzero, the resulting value is called a NaN, short for “not a number.”

当 exponent bits 全为 1 时，显然是过大了的情况，这时候要不是无限（Infinity），要不出现了错误，结果不是个数字 （NaN）

结尾的啰嗦

• 这个标准叫做 IEEE 754，其实哪怕忘了具体内容，也可以把这个名字搬出来直接精神胜利！

• 浮点数之间的比较

  • 由于这种特殊的表示方法，我们有了一个非常便捷比较两个浮点数的方法，直接先比较 sign bits，再看 exponent bits，最后才比较具体的 significant bits。

• 类似的，64 bits ，128 bits 的浮点数，可以举一反三

• 还有个麻烦的地方是浮点数的 Rounding

• Warning：Operations on denormalized floating-point can be tens to hundreds of times slower than on normalized floating-point. This is because many processors can’t handle them directly and must trap and resolve them using microcode.

  • Source：c++ - Why does changing 0.1f to 0 slow down performance by 10x? - Stack Overflow

• Example

  • Source：https://draveness.me/whys-the-design-floating-point-arithmetic/
    
    

Links

• 推荐观看： Fast Inverse Square Root — A Quake III Algorithm - YouTube
• Fast inverse square root
• Information Theory
• RYU Algorithm
• NaN Boxing