Fish Touching🐟🎣

Search

SearchSearch

CRC

Nov 05, 20233 min read

Sender Side (CRC Generator and Modulo Division):

  1. The first step is to add the number of 0 to the data to be sent, calculated using k-1 (k is the bits obtained through the polynomial equation.)
  2. Applying the Modulo Binary Division to the data bit by applying the XOR and obtaining the remainder from the division
  3. The last step is to append the remainder to the end of the data bit and share it with the receiver.
  • Example -  The data bit to be sent is [100100], and the polynomial equation is [x3+x2+1].
  • Data bit - 100100
  • Divisor (k) - 1101 (Using the given polynomial)
  • Appending Zeros - (k-1) > (4-1) > 3
  • Dividend - 100100000
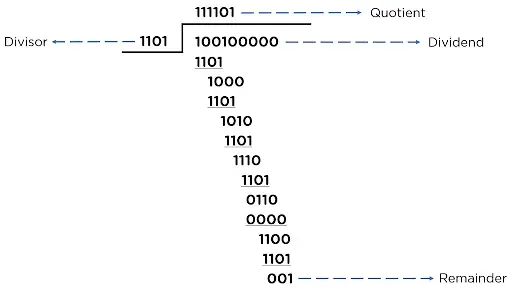
    image.png

Modulo binary division is a method of binary division that uses the modulo operation to find the remainder of a division. In this method, instead of subtracting the divisor from the dividend, we use the XOR operation to find the remainder.

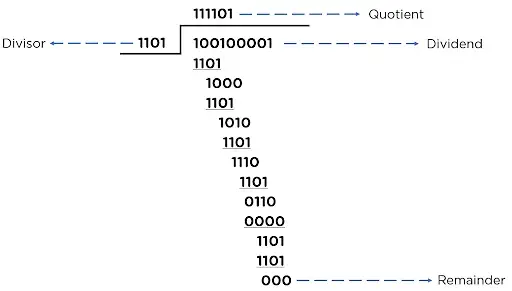
Receiver Side (Checking for Errors in the Received data):

To check the error, perform the Modulo division again and check whether the remainder is 0 or not, 

  1. If the remainder is 0, the data bit received is correct, without any errors.
  2. If the remainder is not 0, the data received is corrupted during transmission.

image.png

CRC32

  • CRC33?

    • Technically, the CRC 32-bit constant 0x04C11DB7 is really a 33-bit constant 0x104C11DB7 which is classified as an IEEE-802 CRC. See RFC 3385

  • When we XOR the data byte into the current CRC value do we start at the top or bottom bits?

  • Which direction do we shift the CRC bits?

  • How do we convert this formula into a table where we handle all 8-bits at once?

  • Reflected = Shift Right

  • The data bytes are fed into the bottom 8 bits of the CRC value

  • We test the bottom-bit of the CRC value

  • We invert the final CRC value

uint32_t crc32_formula_reflect( size_t len, const void *data, const uint32_t POLY = 0xEDB88320 )
{
	const unsigned char *buffer = (const unsigned char*) data;
	uint32_t crc = -1;
 
	while( len-- )
	{
		crc = crc ^ *buffer++;
		for( int bit = 0; bit < 8; bit++ )
		{
			if( crc & 1 ) crc = (crc >> 1) ^ POLY;
			else          crc = (crc >> 1);
		}
	}
	return ~crc;
}
FormPolynomialCRC32 checksum
Normal0x04C11DB70xCBF43926
Reflected0xEDB883200xCBF43926
  1. 初始化 CRC 值 0，反转变 -1
  2. 遍历我们要计算的每个字节，逐位 XOR CRC 值
  3. bits 反转

Graph View

Backlinks