Quicksort

Quicksort

• 单向版本
  1. 取 Pivot，一般为最左 | 最右 | 或者中间随机后和最左右换位置（中间）取最左为 Pivot
  2. 设置变量 i = left - 1 来记录有几个比 Pivot 小（最开始是 0 个小于）
  3. 用循环从左到右遍历除 Pivot 外的所有元素，和 Pivot 进行比较
  4. 如果比 Pivot 大，不动；如果小，则和 i + 1 位置调换，因为 i 是比 Pivot 小的，完成循环
  5. Pivot 和 i + 1 调换，完成左右部分的归纳
  6. 归纳到最后的长度为 1

int partition(int arr[], int low, int high) {
    int pivot = arr[high];    // pivot
    int i = (low - 1);  // Index of smaller element
 
    for (int j = low; j <= high - 1; j++) {
        // If current element is smaller than or equal to pivot
        if (arr[j] <= pivot) {
            i++;    // increment index of smaller element
            swap(&arr[i], &arr[j]);
        }
    }
    swap(&arr[i + 1], &arr[high]);
    return (i + 1);
}
 
void quickSort(int arr[], int low, int high) {
    if (low >= high) {
		return;
    }
	/* pi is partitioning index, arr[p] is now
	   at right place */
	int pi = partition(arr, low, high);
 
	// Separately sort elements before
	// partition and after partition
	quickSort(arr, low, pi - 1);
	quickSort(arr, pi + 1, high);
}

def quicksort(arr, start, end):
    if start < end:
        pivot_index = random.randint(start, end)
        arr[pivot_index], arr[end] = arr[end], arr[pivot_index]
        
        partition_index = partition(arr, start, end)
        
        quicksort(arr, start, partition_index - 1)
        quicksort(arr, partition_index + 1, end)
 
def partition(arr, start, end):
    pivot = arr[end]
    partition_index = start
    for i in range(start, end):
        if arr[i] <= pivot:
            arr[i], arr[partition_index] = arr[partition_index], arr[i]
            partition_index += 1
    arr[partition_index], arr[end] = arr[end], arr[partition_index]
    return partition_index
 
def random_quicksort(arr):
    quicksort(arr, 0, len(arr) - 1)

• 双向版本
  1. 取 0 为 Pivot；1 为 Left；n-1 为 Right
  2. Left, Right 用于记录位置不正确的元素，Left 的值比 Pivot 大，Right 的值比 Pivot 小时，交换并向中靠一步
  3. 直到 Left > Right，交换 Pivot 和 Right（Right 的左边一定比 Pivot 小）

def quicksort(arr, low, high):
    if low < high:
        # Partition the array
        pivot_index = partition(arr, low, high)
        # Recursively apply the quicksort to the sub-arrays
        quicksort(arr, low, pivot_index)
        quicksort(arr, pivot_index + 1, high)
 
def partition(arr, low, high):
    pivot = arr[(low + high) // 2]
    left = low - 1
    right = high + 1
    
    while True:
        # Move right until an element greater than the pivot is found
        left += 1
        while arr[left] < pivot:
            left += 1
 
        # Move left until an element less than the pivot is found
        right -= 1
        while arr[right] > pivot:
            right -= 1
 
        # If the two pointers meet, return the partition point
        if left >= right:
            return right
 
        # Swap the elements on the left and right pointers
        arr[left], arr[right] = arr[right], arr[left]

Python Style:

def quicksort_extra(arr):
    if len(arr) <= 1:
        return arr
    pivot = arr[len(arr) // 2]
    left = [x for x in arr if x < pivot]
    middle = [x for x in arr if x == pivot]
    right = [x for x in arr if x > pivot]
    return quicksort_extra(left) + middle + quicksort_extra(right)

Dual pivot Quicksort

• dual-pivot quicksort

Definition: Pick two elements from the array to be sorted (the pivots), partition the remaining elements into (i) those less than the lesser pivot, (ii) those between the pivots, and (iii) those greater than the greater pivot, and recursively sort these partitions.

---

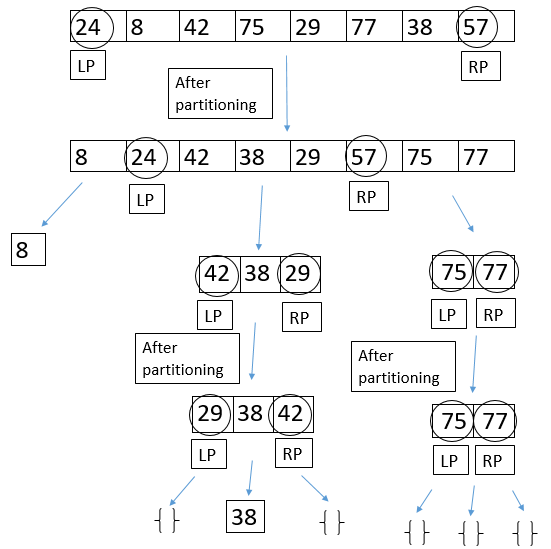
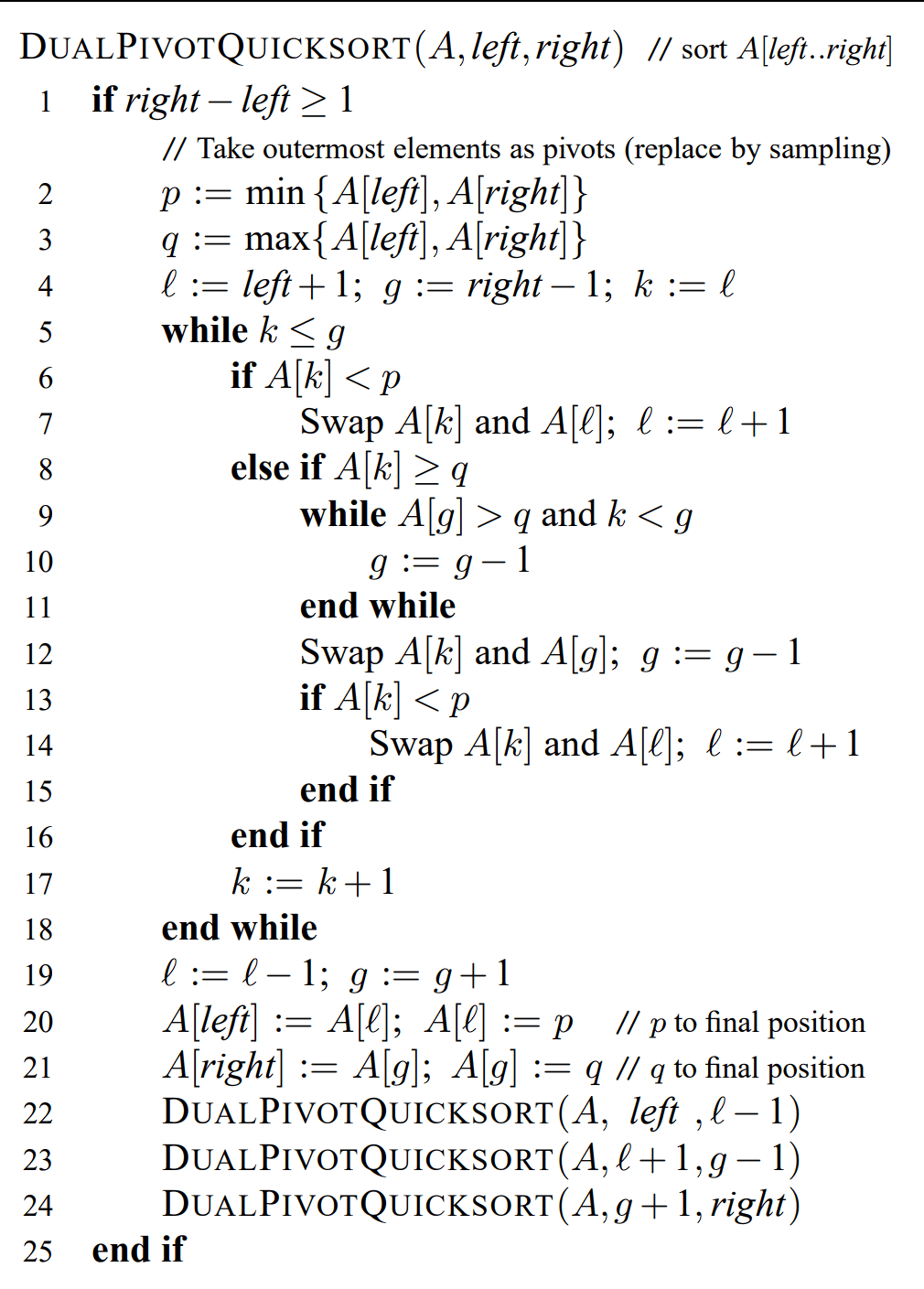
*Note: Dual-pivot quicksort is consistently faster than quicksort* in practice, although classical analysis suggests that it should be slower. *Why Is Dual-Pivot Quicksort Fast? , arXiv:1511.01138 v2 28 Sep 2016.

• Why Quicksort is consider faster than Merge Sort
  It’s “in place sort”, there’s no need to allocate additional memory to complete the task.

Links

• QuickSelect