Gradient descent is an algorithm for finding values of parameters w and b that minimize the cost function J.
\; w &= w - \alpha \frac{\partial J(w,b)}{\partial w} \; \newline
b &= b - \alpha \frac{\partial J(w,b)}{\partial b} \newline \rbrace
\end{align*}$$
where, parameters $w$, $b$ are updated simultaneously. $\alpha$ is the learning rate.
- Gradient:
\begin{align}
\frac{\partial J(w,b)}{\partial w} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)} \tag{4}\
\frac{\partial J(w,b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)}) \tag{5}\
\end{align}
- Learning Rate: How small changes are.
- 
- Convex Function: Bowl shape
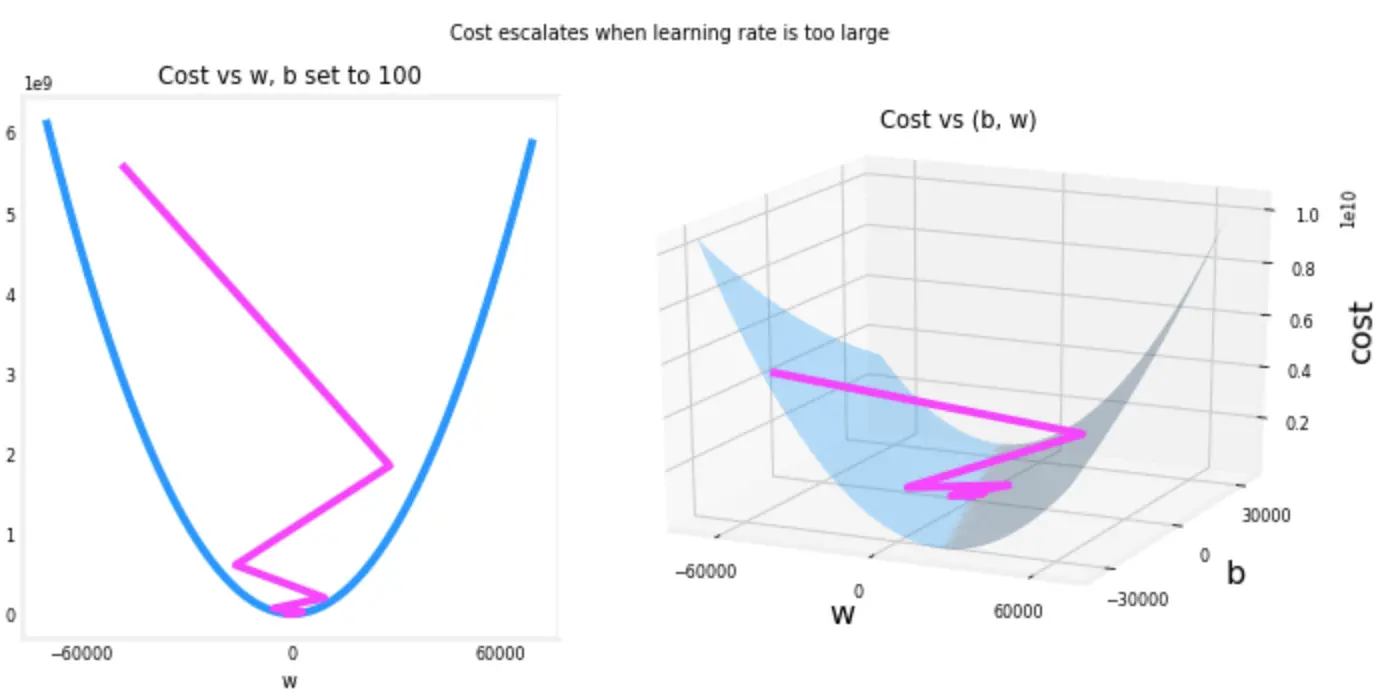
## Learning Rate
- Draw a graph of the cost function to see
- if it converge (**done**)
- if it has some up and down (**bad learning rate**)
## Stochastic Gradient Descent
Stochastic Gradient Descent (SGD) is an optimization algorithm commonly used in machine learning and deep learning for minimizing the loss function. It is a variation of the standard Gradient Descent algorithm that uses only a single or a small random subset of the data (mini-batch) to compute the gradient at each step.