Properties
- Represent 2-3-4 Tree as a Tree.
- Use “internal” red edges for 3- and 4- nodes.
- Require that 3-nodes be left-leaning.

- Disallowed
- right-leaning 3-node representation

- two reds in a row
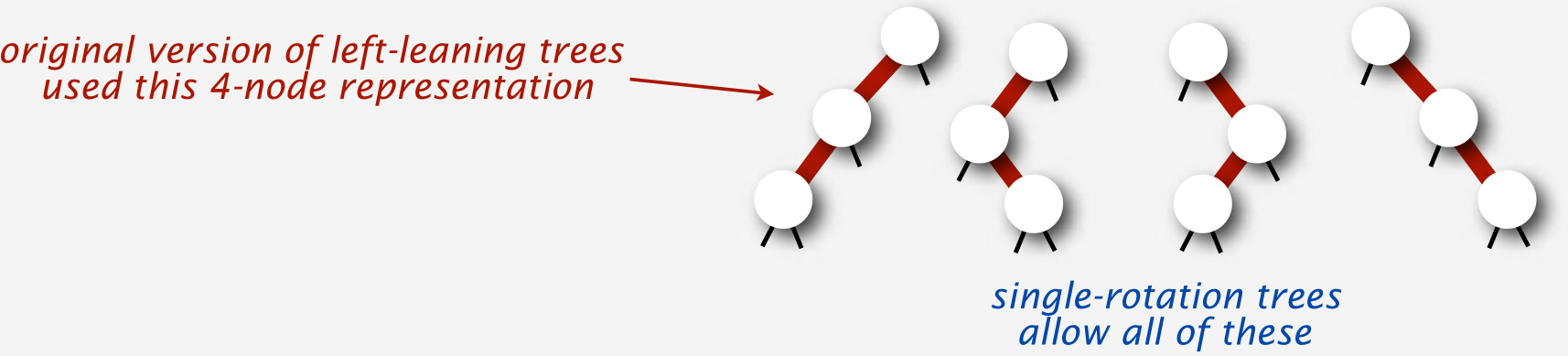
- right-leaning 3-node representation
How to
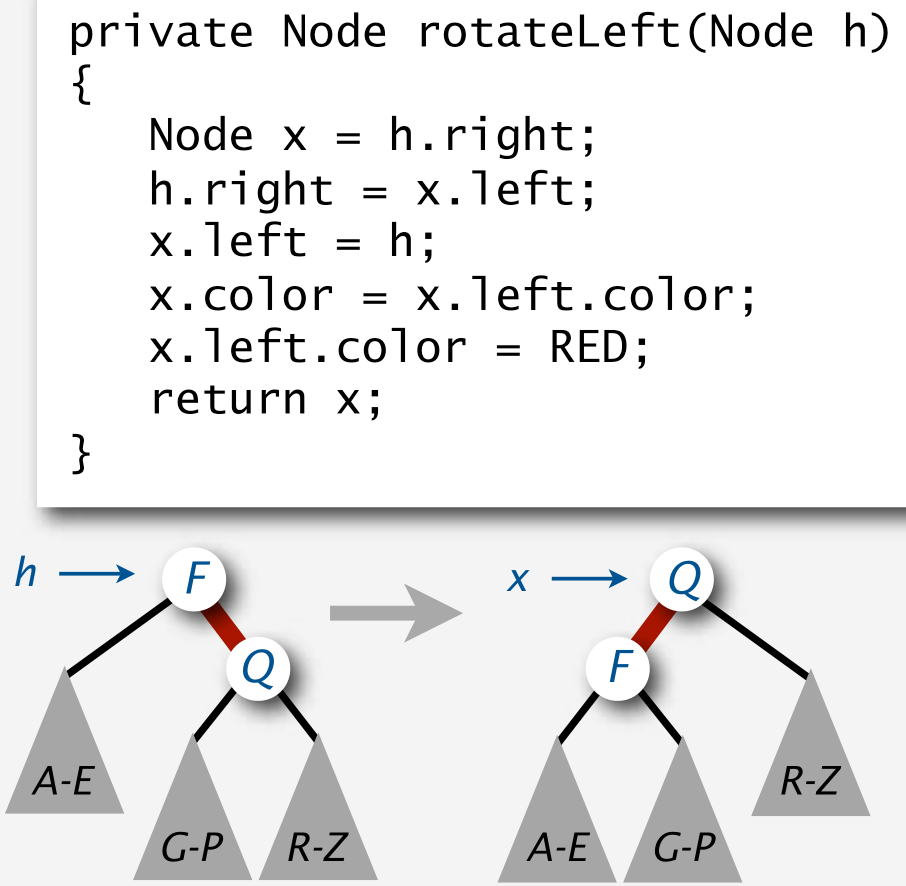
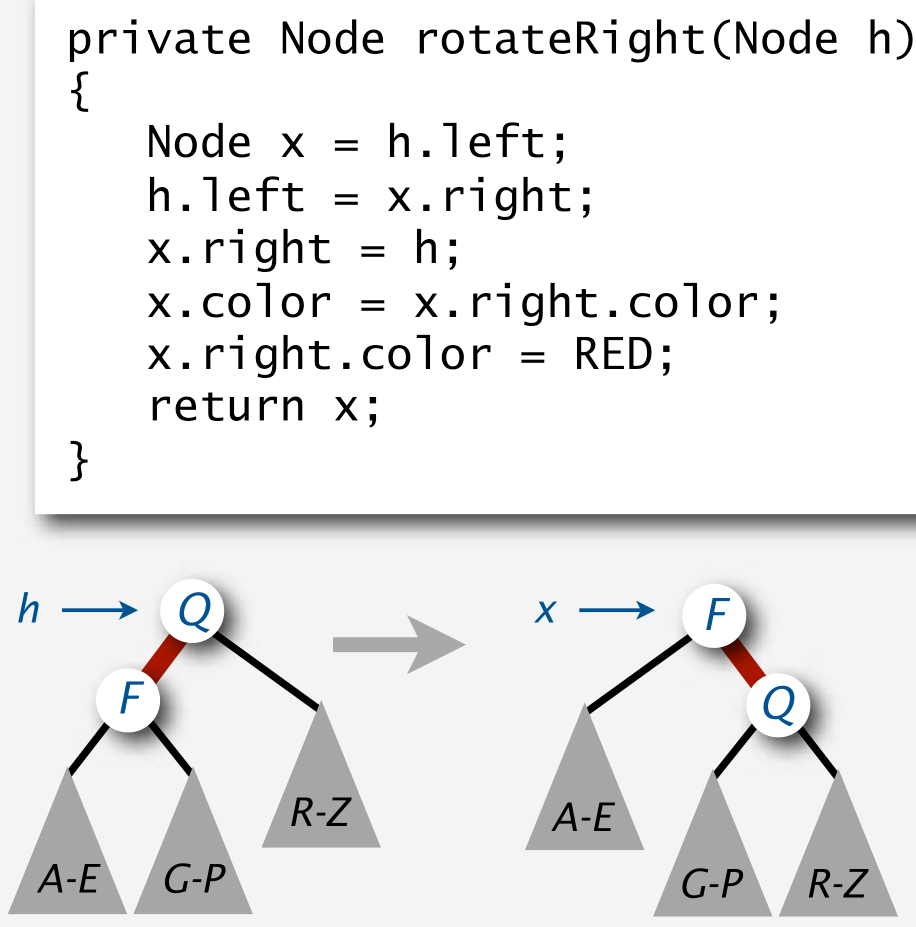
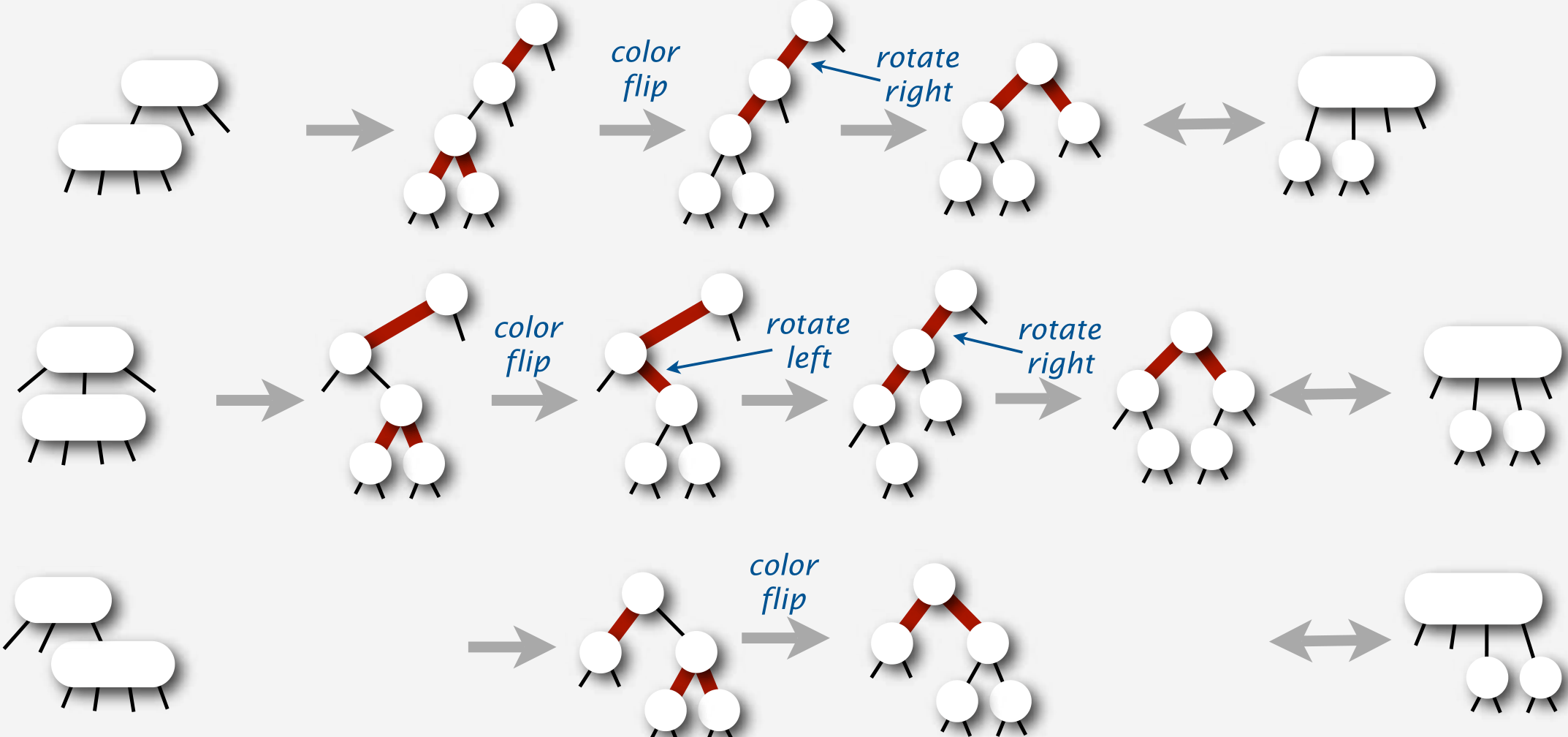
- In Red-Black Tree, we only rotate red links (to maintain perfect black-link balance)
- Left Rotate
- Right Rotate
- Left Rotate
- Then we maintain preperties
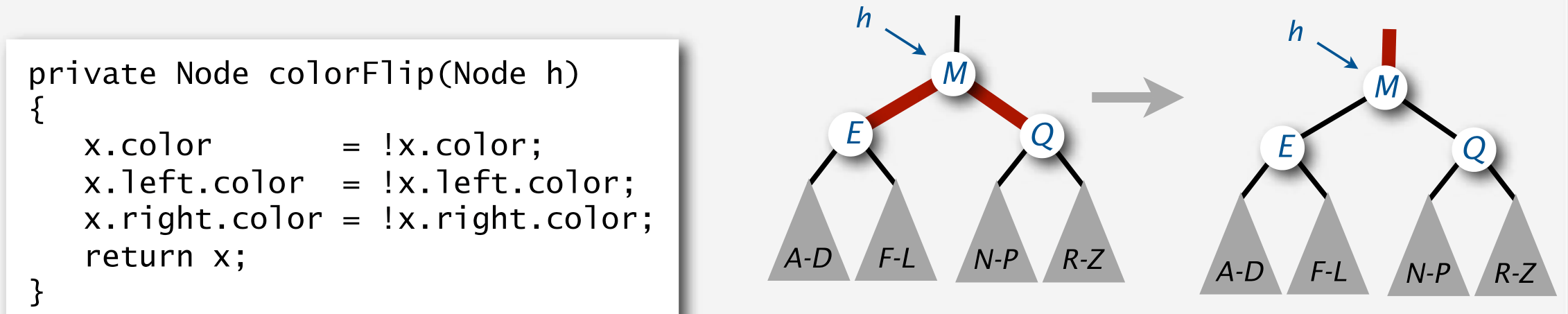
- Color flip to split 4-node
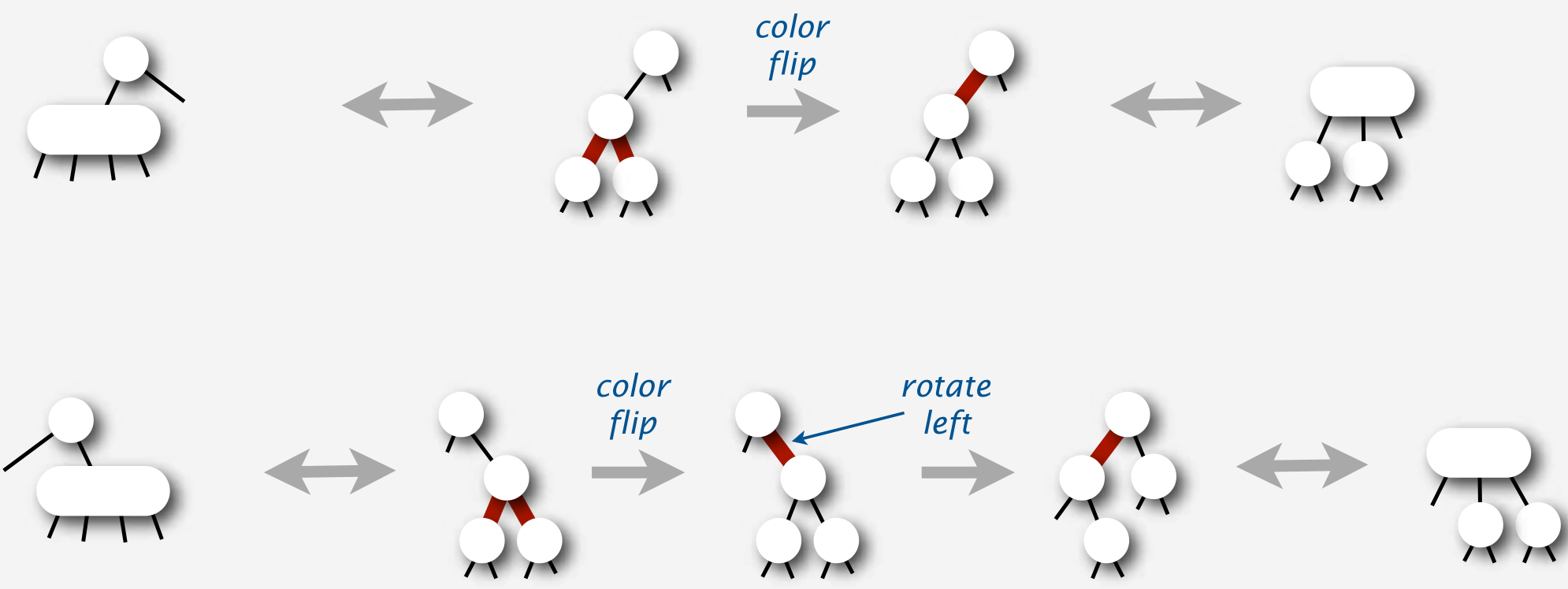
- left-rotate any right-leaning link on search path
- right-rotate top link if two reds in a row found
- trivial with recursion (do it after recursive calls)
- no corrections needed elsewhere
- Color flip to split 4-node
- Insert
- At the bottom

- Split a 4-node

- Enforce left-leaning condition

- Balance a 4-node

- Complete Code (A top-down 2-3-4 nodes tree)

- If we move the color-flipping precedure to the bottom, it becomes a bottom-up 2-3 nodes tree
- At the bottom
Links
Criticism
Sedgewick’s paper is tricky. As of 2013, the insert section presents 2–3–4 trees as the default and describes 2–3 trees as a variant. The delete implementation, however, only works for 2–3 trees. If you implement the default variant of insert and the only variant of delete, your tree won’t work. The text doesn’t highlight the switch from 2–3–4 to 2–3: not kind.