Floating Point Representation

Blog: Introduction to Floating Point Number

• sign s
  • negative: s=1
  • positive: s=0
• exponent E
  • weights the value by a (possibly negative) power of 2
• significand M
  • fractional binary number ranges between 1 and $2-ϵ$ (Normalized) or between 0 and $1-ϵ$ (Denormalized)
• result V
  • $2^E\ast M$

---

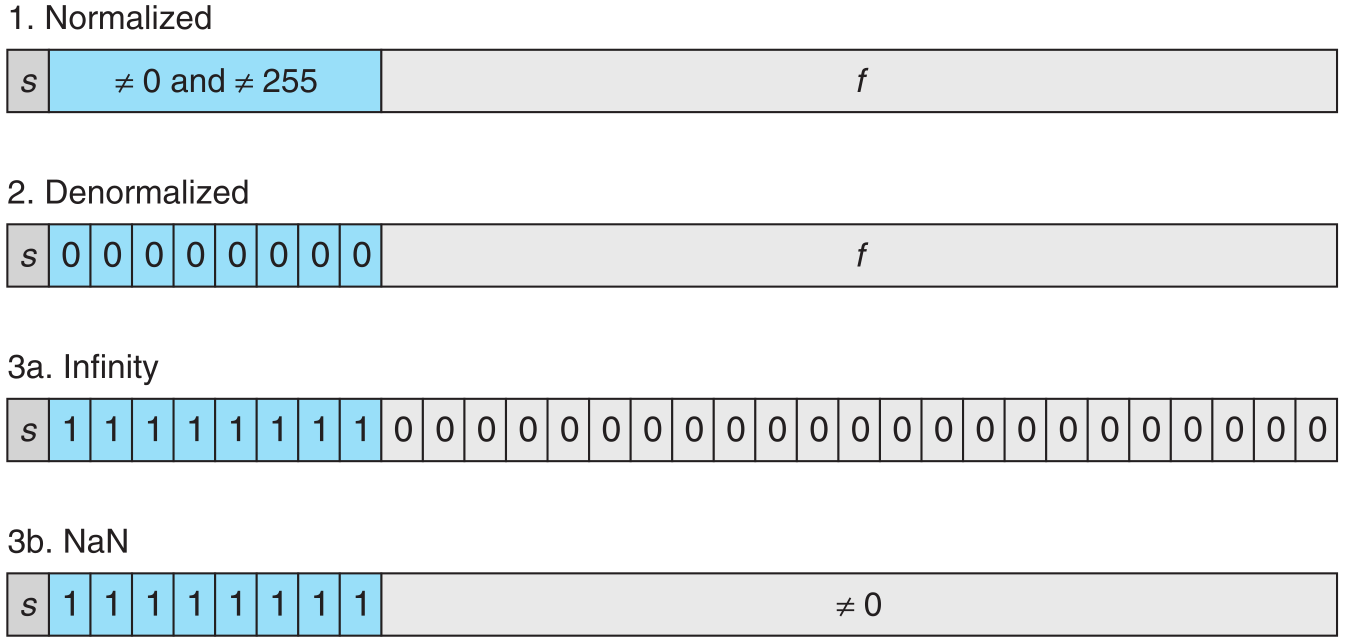
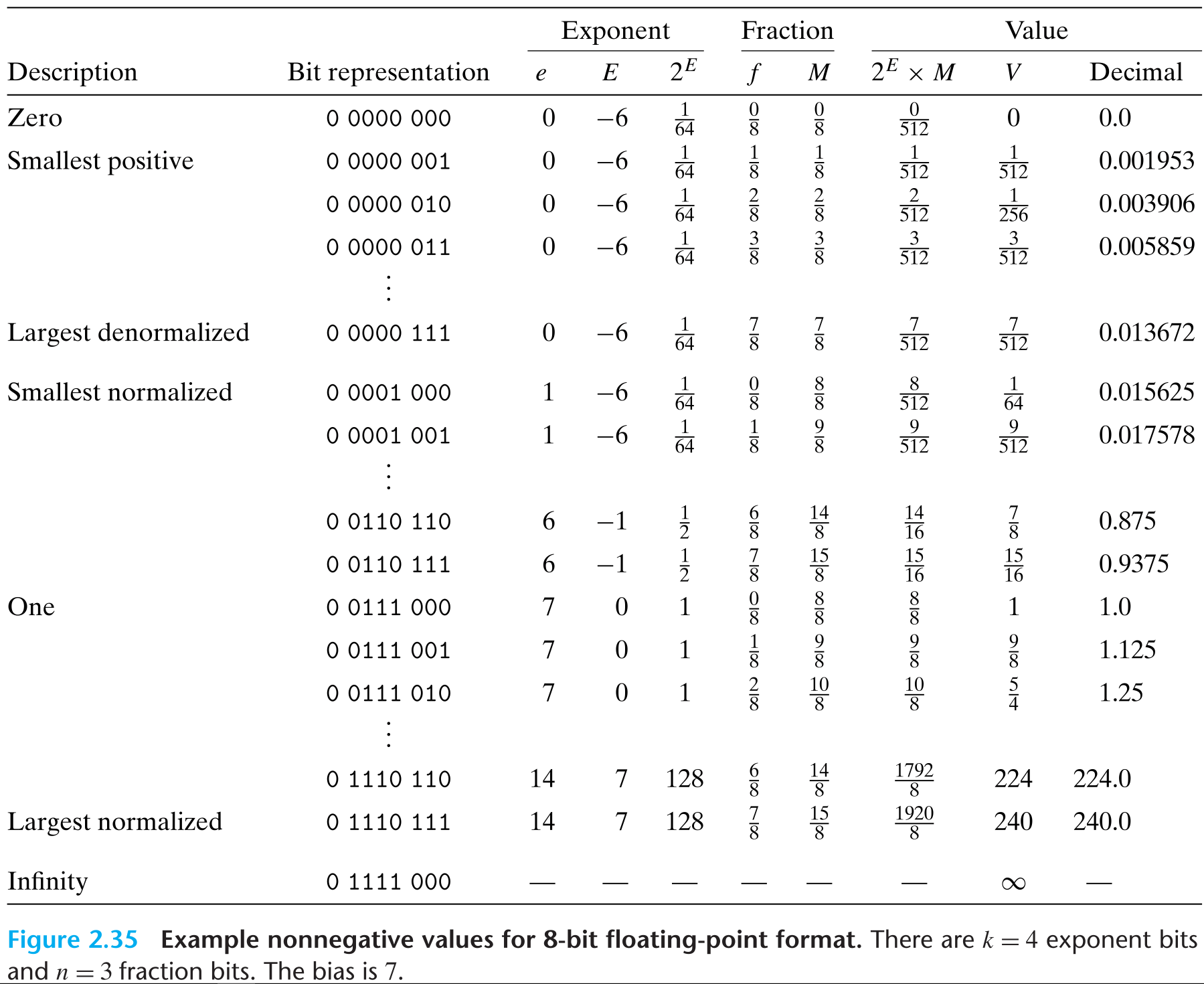
Case 1: Normalized Values

• When bit pattern of exp is neither all zeros nor all ones. Then the exponent field is interpreted as in biased form.
• The exponent value is $E=e-Bias$
  • where e is the unsigned number having bit representation $e_{k-1}\cdots e_1{e}_0$,
  • and Bias is a bias value $2^{k-1}-1$ (where k is the number of bits in the exponent, 127 for single precision and 1023 for double)
  • This yields exponent ranges from −126 to +127 for single precision and −1022 to +1023 for double precision.
• The fraction field frac is interpreted as representing the fractional value f, where $0\le f<1$, having binary representation $0.f_{n-1}\cdots f_1{f}_0$ .
  • The significand is defined to be $M=1+f$
  • This is sometimes called an implied leading 1 representation, because we can view M to be the number with binary representation $1.f_{n-1}\cdots f_1{f}_0$
  • This representation is a trick for getting an additional bit of precision for free, since we can always adjust the exponent E so that significand M is in the range $1\le M<2$ . We therefore do not need to explicitly represent the leading bit, since it always equals 1.

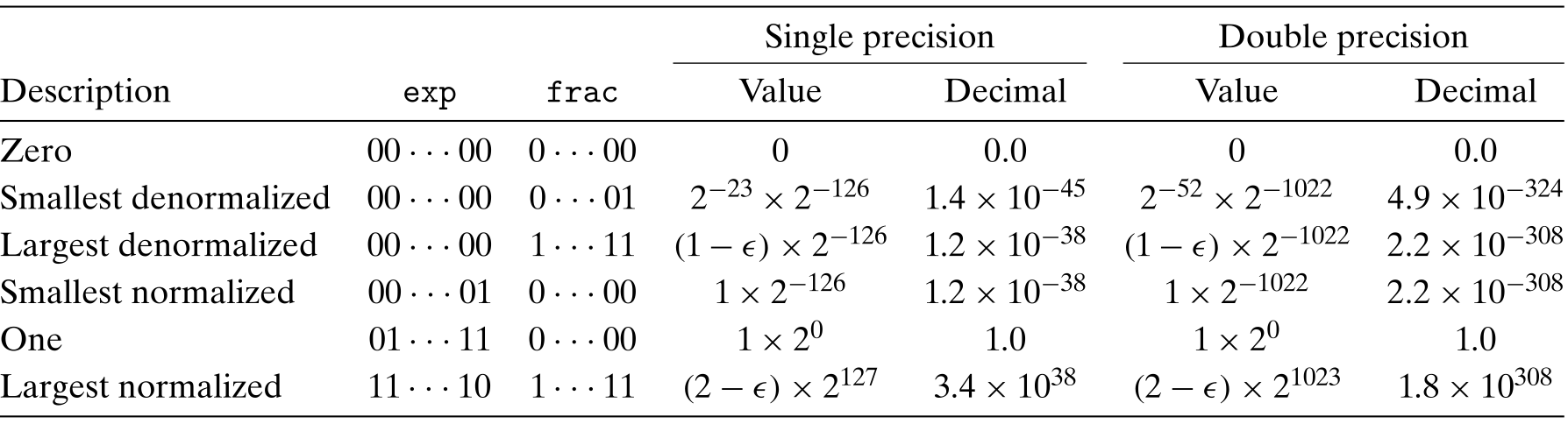
Case 2: Denormalized Values

When the exponent field is all zeros, the represented number is in denormalized form.
the exponent value is $E=1-Bias$, and the significand value is $M=f$ , that is, the value of the fraction field without an implied leading 1.

• Why?
  • they provide a way to represent numeric value 0, since with a normalized number we must always have $M\ge 1$ , and hence we cannot represent 0. We even have +0.0 and -0.0
  • represent numbers that are very close to 0.0. They provide a property known as gradual underflow in which possible numeric values are spaced evenly near 0.0.

Case 3: Special Values

• When the exponent field is all ones
  • When the fraction field is all zeros, the resulting values represent infinity
  • When the fraction field is nonzero, the resulting value is called a NaN, short for “not a number.”

NaN

• signalling NaNs

  • the highest mantissa bit is 0

• quiet NaNs

  • otherwise

• Intel’s QNaN Floating-Point Indefinite

• NaN Boxing

• Optimization · Crafting Interpreters

Example

Links

• NaN Boxing
• Floating Point Rounding