Graph Theory

• Floyd Algorithm
• 简单图：不含平行边、环（自环）的图。
• 联通图：任何两个顶点都联通（所有点相互可达）
• 平凡图：1 阶零图 $N_1$ （只有 1 个点、没有边的图）
• 完全图：所有顶点相邻 (n-1)
• 基图：将有向图的所有的有向边替换为无向边，所得到的图称为原图的基图。
• 弱连通图：如果一个有向图的基图是连通图，则有向图是弱连通图。
• 强连通图：在有向图中, 若对于每一对顶点 v1 和 v2, 都存在一条从 v1 到 v2 和从 v2 到 v1 的路径

Chap14 图的基本概念

• 握手定理

  • 握手定理：
    • 无向图：顶点度数之和为边数两倍
    • 有向图：入度=出度=边数
    • 任何图：奇数顶点个数是偶数

  Link to original

• 度数列：顶点度数的排列

• 零图：只有结点没有边的图

• Isomorphism

• k- 正则图：所有点度数列均为 k

• 补图：一个图有着跟 G 相同的点，边为 G 中没有的。

• 子图：点和边是包含关系

  • A subgraph of a graph G is another graph formed from a subset of the vertices and edges of G. The vertex subset must include all endpoints of the edge subset, but may also include additional vertices.
  • A spanning subgraph is one that includes all vertices of the graph;
  • an induced subgraph is one that includes all the edges whose endpoints belong to the vertex subset.
  • 真子图：真包含
  • 生成子图：点集相同的子图
  • 导出的子图：
    • 顶点导出：如果原本的两个顶点间有边，子图中有边。
    • 边导出：边的顶点还是边的顶点

• 联通分支：$p(G)$ ，内部相连的图个数

• 割集

  • 点割集：去掉点后分为两个图的顶点的集合 V′ ，若只有一个点 v，v 是 割点。
    • (点)连通度: $\kappa (G)=min(|V^{\prime }||V^{\prime }为G的点割集)$, 完全图 Kn 的点连通度为 n − 1，非连通图的连通度为 0。
  • 边割集：去掉点后分为两个图的顶点的集合 E’
    • 边 连通度: $\lambda (G)$
  • $\kappa (G)\le \lambda (G)\le \delta (G)$

• $\Gamma$ 是路径，其始点和终点都不与 $\Gamma$ 外的顶点相邻（全部包围）

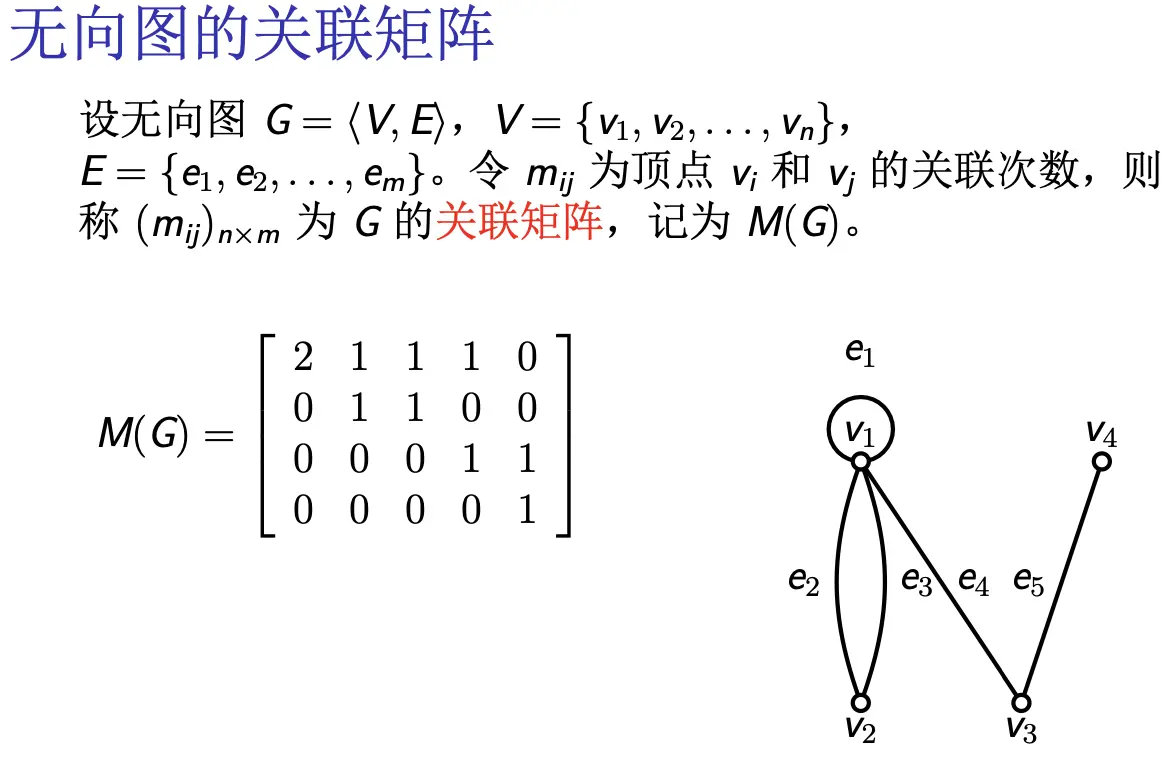
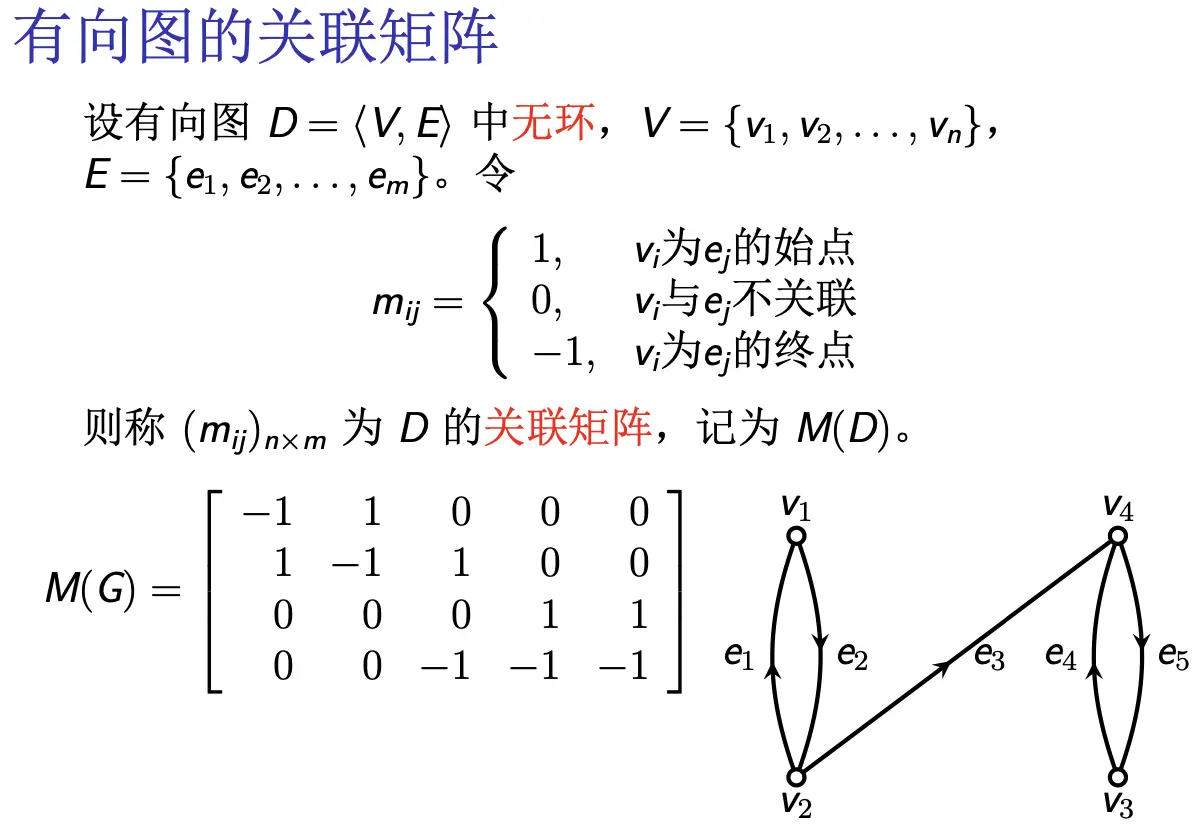
• 关联矩阵：顶点 i 和边 j 的关联次数（环算 2）(Vertex x Edge)

  • 无向图:
  • 有向图：

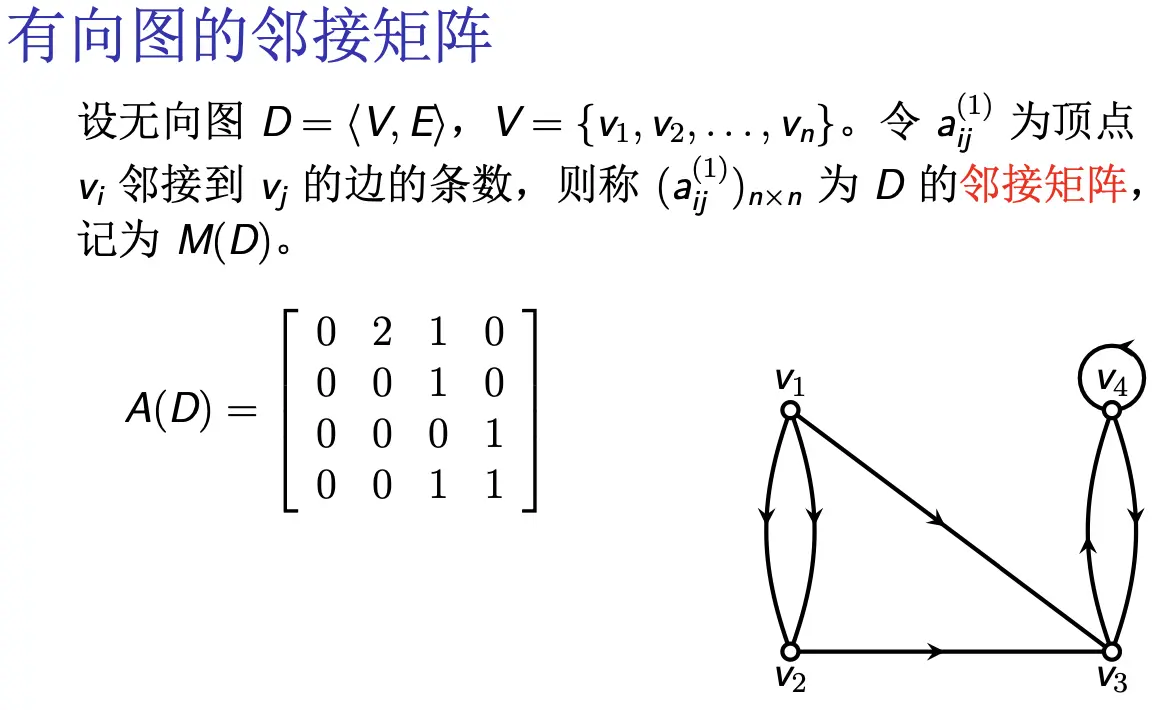
• 邻接矩阵：顶点 i 邻接 到顶点 j 的边数。(Vertex x Vertex)

  • 有向图：

Chap15 欧拉图与哈密顿图

欧拉图

欧拉图

• 欧拉图
  • 欧拉通（回）路：通过图中所有边一次，且仅一次行遍所有顶点的通（回）路
  • 欧拉图：有欧拉回路
  • 半欧拉图：有欧拉通路而无欧拉回路
• 欧拉图判定：
  • 无向
    • G 的所有顶点的度数都是偶数
    • G 是若干个边不重的圈的并
  • 有向
    • D 的所有顶点的出度和入度相等;
    • D 是若干个边不重的有向初等回路的并。
• 半欧拉图判定：
  • 无向
    • 当且仅当 G 是连通的，且恰好只有两个奇度顶点（始，终）。
  • 有向
    • 当且仅当 D 是单向连通的且恰好有两个奇度顶点，其中一个奇度顶点的入度比出度大 1（终点），另一个 奇度顶点的出度比入度大 1（起点），而其余顶点的入度等于出度。

Link to original

---

• 二部图：把 V 分成 V1， V2， 使得 G 中每条边两个端点一个属于 V1，一个属于 V2，记作 <V1, V2, E>，无向图是二部图当且仅当它没奇圈

• 完全二部图：G 是简单图，V1 中顶点和 V2 所有 顶点相邻，记作 $K_{r,s}$ r = |V1| s = |V2|

• 哈密顿图

  哈密顿图

  • 哈密顿图
    • 哈密顿通（回）路：通过图中所有顶点一次的通（回）路
    • 具有哈密顿回路的图称为哈密顿图;
    • 具有哈密顿通路而无哈密顿回路的图称为半哈密顿图;
    • 二部图 |V1| ≥ |V2| ≥ 2，性质有：
      • G 是哈密顿图，则 |V1| = |V2|
      • G 是半哈密顿图，则 |V1| = |V2| + 1;
      • |V1| ≥ |V2| + 2，则 G 既不是哈密顿图，也不是半哈密顿图。
  • 哈密顿图判定
    • 无向
      • 必要（哈密顿图性质）
        • 对于任意非空的顶点集 V1 ⊂ V，均有 p(G − V1) ≤ |V1|。
      • 充分（存在哈密顿回路）
        • G 是 n 阶简单无向图，对于任意不相邻的顶点 vi 和 vj 均有 d(vi)+d(vj) ≥ n
  • 半哈密顿图判定
    • 无向
      • 必要
        • 对于任意非空的顶点集 V1 ⊂ V，均有 p(G − V1) ≤ |V1| + 1。
      • 充分（存在哈密顿通路）
        • G 是 n 阶简单无向图，对于任意不相邻的顶点 vi 和 vj 均有 d(vi)+d(vj) ≥ n−1

  Link to original

Chap16 树

• 森林：每个连通分支都是树的无向图
• 无向树：m = n−1;（m：边数，n：阶）
• 生成树 T：无向图 G 的生成子图 T 是树
  • 存在条件：无向图 G 具有生成树，当且仅当 G 是连通图。
  • T 的所有弦的导出子图为 T 的余树，记为 $\bar{T}$
  • G 为 n 阶 m 条边的无向连通图，则 m ≥ n−1;
  • $\bar{T}$ 是 G 的生成树 T 的余树，则 $\bar{T}$ 的边数为 m−n+1;
  • 弦：非生成树的边，但在 G 中
• 基本回路系统：
  • 基本圈（回路）$C_r$：添加弦 $e_r$ 后生成的圈
  • 基本回路系统：{C1,C2,…,Cm−n+1}
  • 圈秩：m−n+1，即集合秩
• 基本割集系统
  • 基本割集 $S_i$ : T 的对应树枝 $e_i$ 和弦构成的割集
  • 基本割集系统：{S1,S2,…,Sn−1}
  • 割集秩：n-1
• 最小生成树：Greedy 避圈 (Kruskal Algorithm)
• Huffman Tree

Chap17 平面图

• 平面图: 将无向图 G 画在平面上，并且使得除顶点外无边相交
• 非平面图：$K_5$, $K_{3,3}$, $K_n(n\ge 6)$, $K_{3,n}(n\ge 4)$
• 平面图判定：一个简单图是平面图当且仅当它不是 K5 或 K3,3 的次图，一个图的次图是将它做有限多次的取子图 (删除部分顶点和边) 和做 边收缩(将某边缩成一个顶点) 所得到的图。
• 面和边界
  • 面：被边划分的区域
  • 边界：包围每个面的所有边组成的 回路组
  • 次数：面 R 的边界数（长度）（桥计算两次）
  • 定理：平面图所有面的次数之和等于边个数的两倍。
• 极大平面图：设 G 为简单平面图，若在 G 的任意两个不相邻的顶点之间 加上一条边，所得图为非平面图
  • K1, K2, K3, K4, K5 − e 都是极大平面图;
  • 极大平面图是连通的
  • 阶数大于等于 3 的极大平面图没有割点和桥。
  • G 是 $n\ge 3$ 的简单联通平面图，G 为极大平面图 iff G 每个面次数为 3
  • G 是 $n\ge 3$ 阶 m 条边的极大平面图，则 $m=3n-6$
  • G 是 $n\ge 3$ 阶 m 条边的简单平面图，则 $m\le 3n-6$
• 欧拉公式：
  • 连通平面图：G 为 n 阶 m 条边 r 个面，则 n − m + r = 2 (k = 1)
    • 每个面的次数至少为 l >=3, $m\le \frac{l}{l-2}(n-2)$ ($l\ge 3$)
  • 非连通图：G 为 n 阶 m 条边 r 个面的平面图。若 G 有 k 个连通分支，则 n − m + r = k + 1
    • 每个面的次数至少为 l >=3, $m\le \frac{l}{l-2}(n-k-1)$ ($l\ge 3$)