GCD

Divisor

A divisor of n, also called a factor of n, is an integer m that can be multiplied by some integer to produce n.
and n is a multiple of m.
$n=km$ then $m|n$

GCD

Greatest common divisor. It is also termed as the highest common factor (HCF) or the greatest common factor (GCF).
Euclidean algorithm - Wikipedia

Properties

• $gcd(a,b)=ar+bs$ Bezout’s Identity
• If $gcd(a,n)=1$ and $gcd(a,m)=1$ then $gcd(a,mn)=1$
• Lamé’s Theorem:
  • If Euclid’s Algorithm requires k steps to compute the gcd of some pair, then the smaller number in the pair must be greater than or equal to the kth Fibonacci number.
  • $n\ge Fib(k)\approx \frac{{\varphi }^k}{\sqrt{5}}$, order of growth is $\Theta (\log n)$
    • n is the smaller of the two inputs to the procedure
    • k is the number of steps taken by the process

Method 1: Prime Factorizations

to compute $gcd(48,180)$, we find the prime factorizations $48=2^4\cdot 3^1$ and $180=2^2\cdot 3^2\cdot 5^1$; the GCD is then $2^{min(4,2)}\cdot 3^{min(1,2)}\cdot 5^{min(0,1)}=2^2\cdot 3^1\cdot 5^0=12$
I Do Maths · Prime Numbers and Prime Factorization

Method 2: Euclidean Algorithm

The Euclidean Algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number.

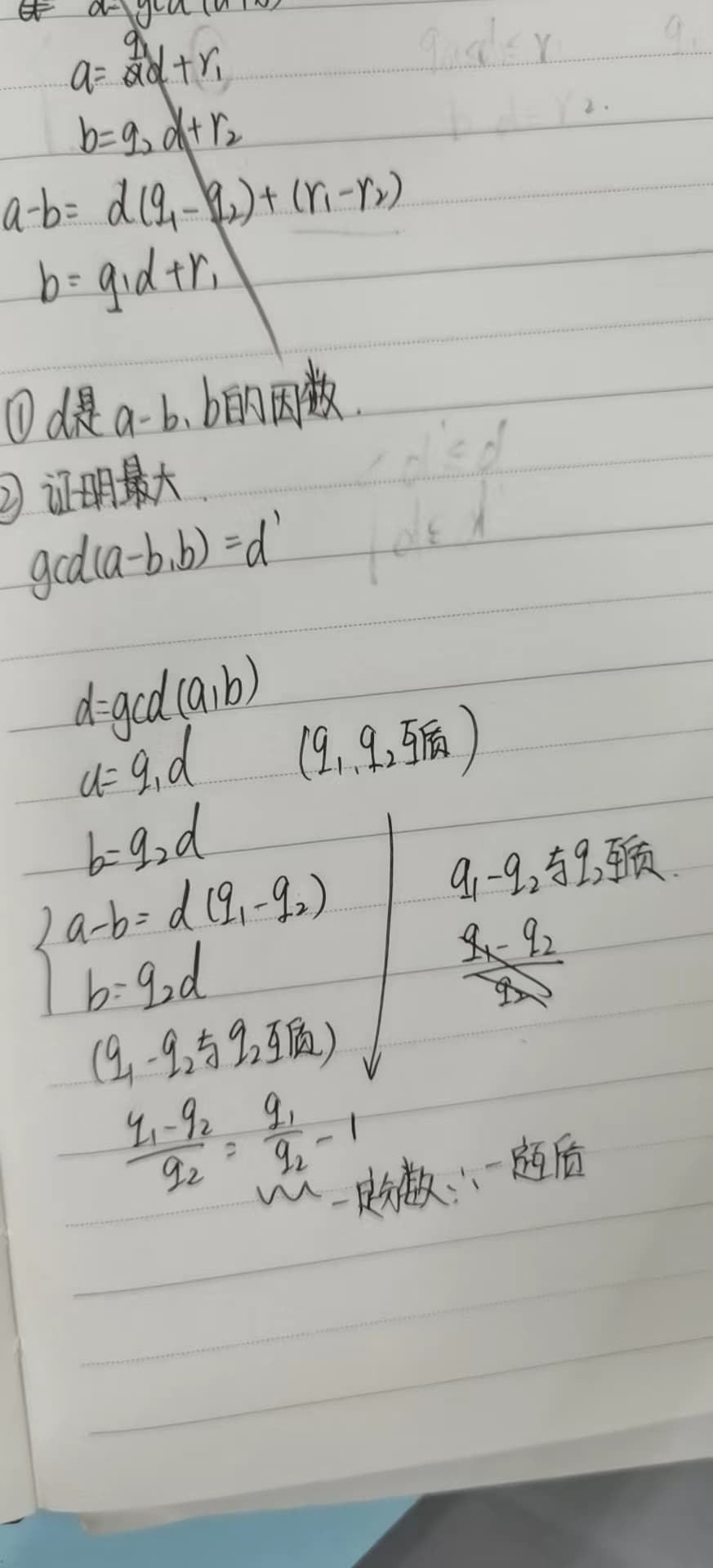
Code for GCD

int gcd(int a, int b)
{
	if (b == 0)
		return a;
	else
		return gcd(b, a % b);
}

1. gcd(0, v) = v, because everything divides zero, and v is the largest number that divides v. Similarly, gcd(u, 0) = u.
2. gcd(2u, 2v) = 2 · gcd(u, v)
3. gcd(2u, v) = gcd(u, v), if v is odd (2 is not a common divisor). Similarly, gcd(u, 2v) = gcd(u, v) if u is odd.
4. gcd(u, v) = gcd(|u − v|, min(u, v)), if u and v are both odd.

Links

• Bezout’s Identity