B Tree

B+ Tree
Application: File System (Ext4)

Introduction

B-trees are balanced search trees designed to work well on disk drives or other direct-access secondary storage devices. B-trees are similar to red-black trees (Chapter 13), but they are better at minimizing the number of operations that access disks. Many database systems use B-trees, or variants of B-trees, to store information. —CLRS

It only read one node into memory, so it is useful for databases which mostly have larger table size than memory capacity.

Properties

Every node x has the following attributes.
1. x.n: the number of keys
2. x.keys: in monotonically increasing order
3. x.leaf: boolean value
Each node x contains x.n + 1 pointers to its children. Leaf nodes have no children.
The keys x.key_i separate the ranges of keys stored in each subtree. Just like a 2-3-4 Tree
All leaves have the same depth, which is the height h
Nodes have a lower and upper bounds on the number of keys they can contain (t is an arbitrary constant representing the lower and upper bounds).
1. Every node other than the root must have at least t-1 keys. Thus nodes have at least t children.
2. Every node may contain at most 2t - 1 keys. Thus nodes may have at most 2t children. Which we call it full.
$h \leq lo g_{t} \frac{n + 1}{2}$

Operations

The root of the B-tree is always in main memory, so that no procedure ever needs to perform a DISK-READ on the root. If any changes to the root node occur, however, then DISK-WRITE must be called on the root.
Any nodes that are passed as parameters must already have had a DISK-READ operation performed on them

Search

Search makes a multiway branching decision according to the number of the node’s children. More precisely, at each internal node x , the search makes an (x.n + 1)-way branching decision.

B-Tree-Search(x, k) // x is the node, k for key
	i = 1
	while i <= x.n and k > x.key_i // find the right interval
		i += 1
	if i <= x.n and k == x.key_i
		return (x, i)
	elseif x.leaf
		return nil
	else DISK-READ(x.c_i)
		return B-Tree-Search(x.c_i, k)

$O (t h)$

Insertion

Create Empty Tree

ALLOCATE-NODE: allocates one disk block to be used as a new node in O(1) time

B-Tree-Create(T)
	x = ALLOCATE-NODE()
	x.leaf = True
	x.n = 0
	DISK-WRITE(x)
	T.root = x

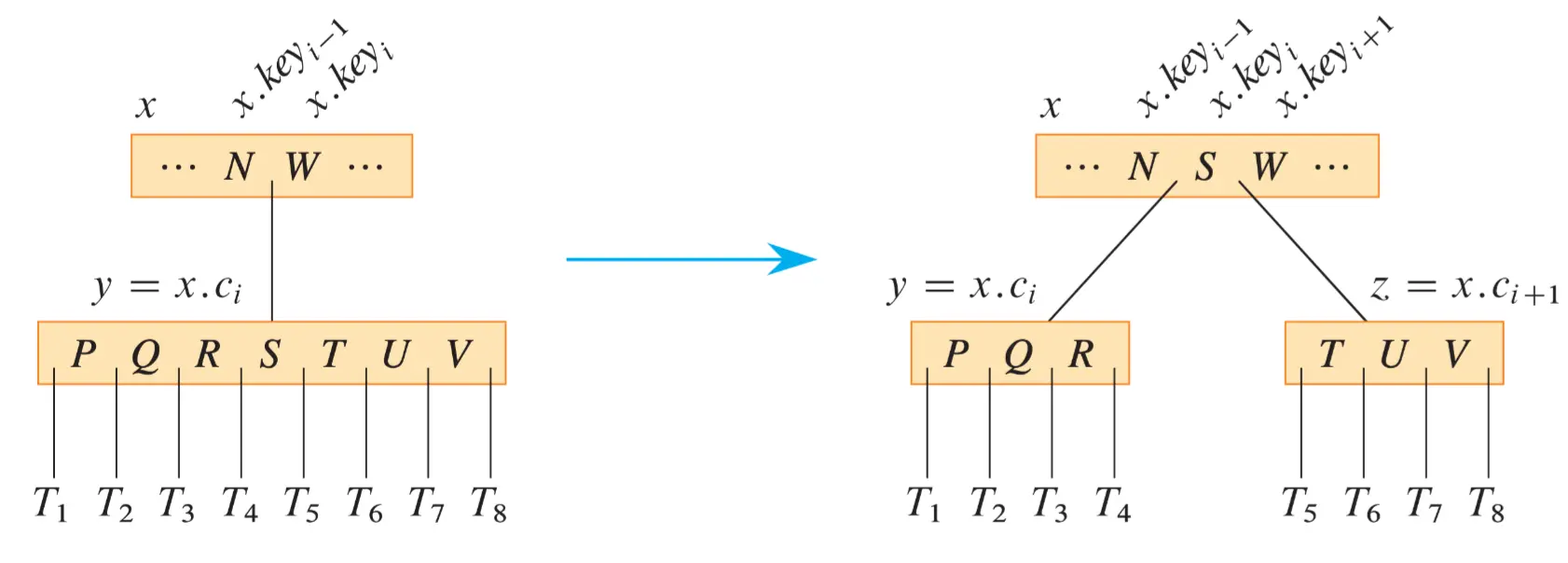
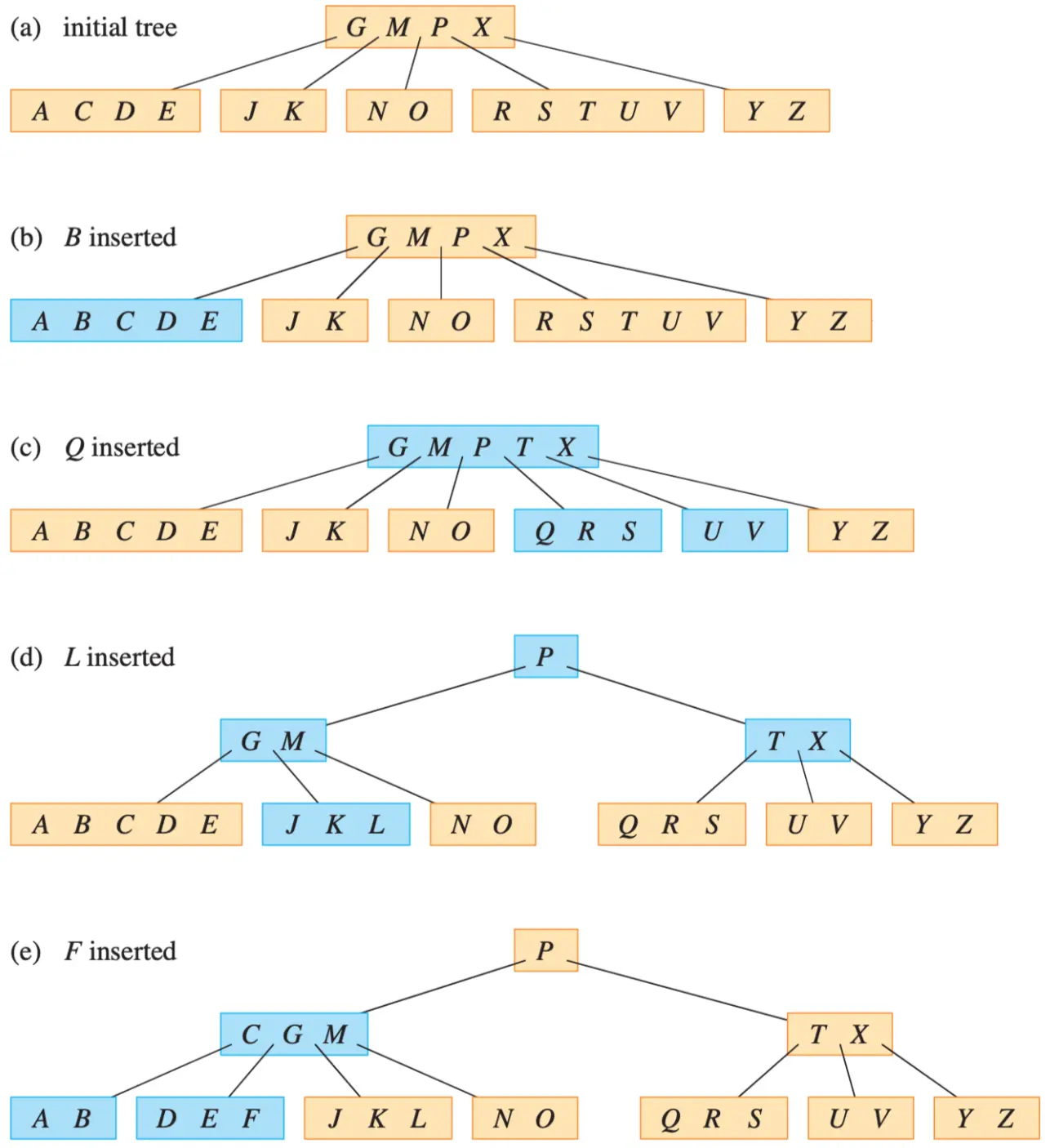
Splitting a Node in a B-tree

Insert the new key into an existing leaf node. Since you cannot insert a key into a leaf node that is full, you need an operation that splits a full node y (having 2t - 1 keys) around its median key y.key_t into two nodes having only t - 1 keys each.
To avoid having to go back up the tree, just split every full node you encounter as you go down the tree. In this way, whenever you need to split a full node, you are assured that its parent is not full. Inserting a key into a B-tree then requires only a single pass down the tree from the root to a leaf.

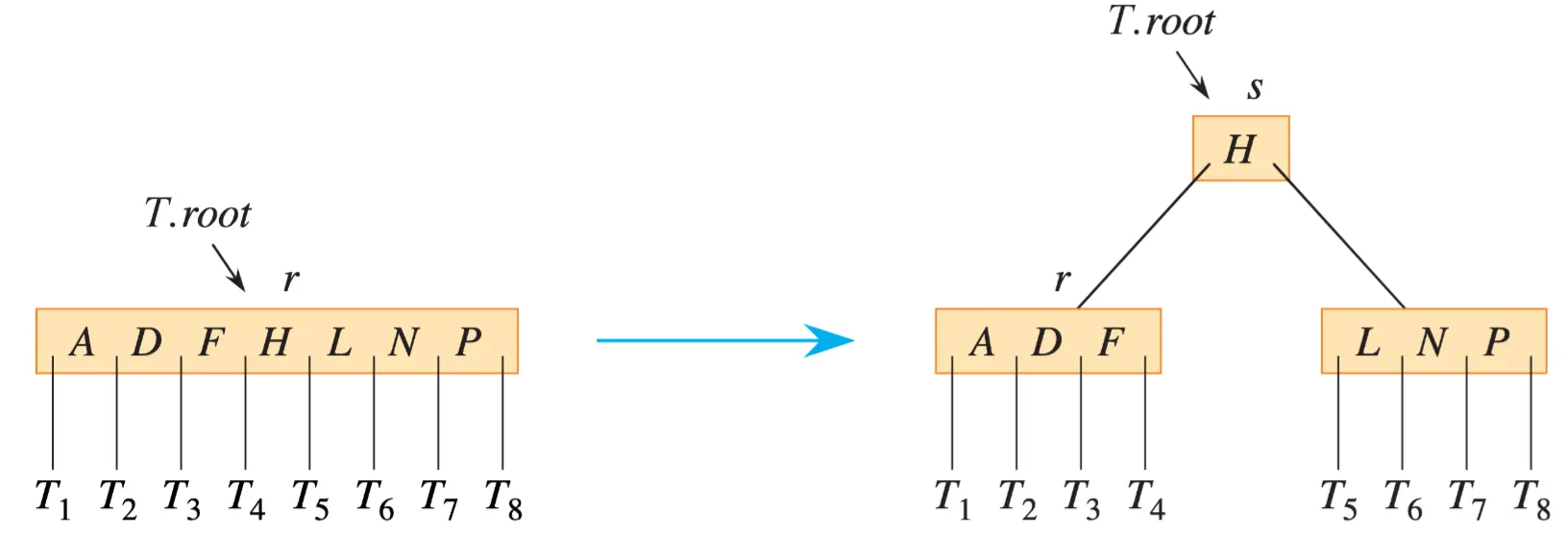
To split a full root, you first need to make the root a child of a new empty root node, so that you can use B-TREE-SPLIT-CHILD. The tree thus grows in height by 1: splitting is the only means by which the tree grows taller.

B-Tree-Split-Child(x, i)
	y = x.c_i // y(x's ith child) is the full node to split
	z = ALLOCATE-NODE() // z will take half of y
	z.leaf = y.leaf
	z.n = t - 1
	for j = 1 to t-1
		z.key_j = y.key_j+t // z gets y's greater parts
	if not y.leaf
		for j = 1 to t
			z.c_j = y.c_j+t // z also get the splited node's children
	y.n = t - 1 // y keeps t - 1 keys
	for j = x.n + 1 downto i+1 // shift parent's(x's) children to the right
		x.c_j+1 = x.c_j
	x.c_i+1 = z // make z a new child
	for j = x.n downto i
		x.key_j+1 = x.key_j // shift the keys in x
	x.key_i = y.key_i // insert y's median key
	x.n = x.n + 1 // x has a new child
	DISK-WRITE(y)
	DISK-WRITE(z)
	DISK-WRITE(x)

Split Root

B-Tree-Split-Root(T)
	s = ALLOCATE-NODE()
	s.leaf = FALSE
	s.n = 0
	s.c_1 = T.root
	T.root = s
	B-Tree-Split-Schild(s, 1)
	return s

Insert Procedure

Inserting a key k into a B-tree T of height h requires just a single pass down the tree and O(h) disk accesses. The CPU time required is O(th) = O(t log t n).
The B-TREE-INSERT procedure uses B-TREE-SPLIT-CHILD to guarantee that the recursion never descends to a full node. If the root is full, B-TREE-I NSERT splits it by calling the procedure B-TREE-SPLIT-ROOT on the facing page

B-Tree-Insert(T, k)
	r = T.root
	if r.n == 2t - 1
		s = B-Tree-Split-Root(T)
		B-Tree-Insert-Nonfull(s, k)
	else
		B-Tree-Insert-Nonfull(r, k)

B-Tree-Insert-Nonfull(x, k)
	i = x.n // search from right to left
	if x.leaf // inserting into a leaf
		while i >= 1 and k < x.key_i // right shift keys in x to make room for k
			x.key_i+1 = x.key_i
			i -= 1
		x.key_i+1 = k // insert key k in x
		x.n += 1 // have 1 more key
		DISK-WRITE(x)
	else // find the child where k belongs
		while i >= 1 and k < x.key_i
			i -= 1
		i += 1 // position located
		DISK-READ(x.c_i)
		if x.c_i.n == 2t-1 // split the child if it's full
			B-Tree-Split-Child(x, i)
			if k > x.key_i // k go into x.c_i ro x.c_i+1
				i += 1
		B-Tree-Insert-Nonfull(x.c_i, k)

Complexity: $O (t h)$

Deletion

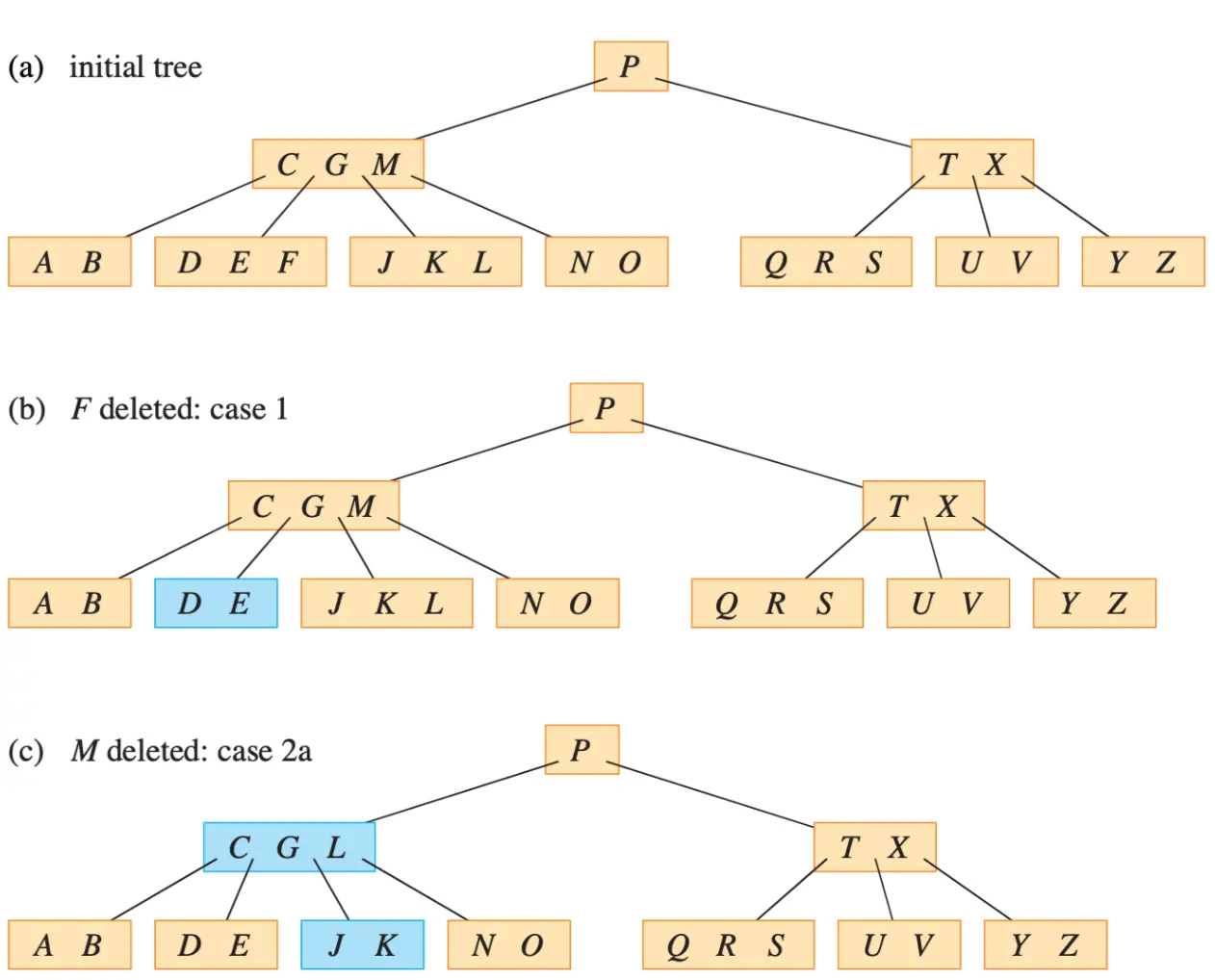
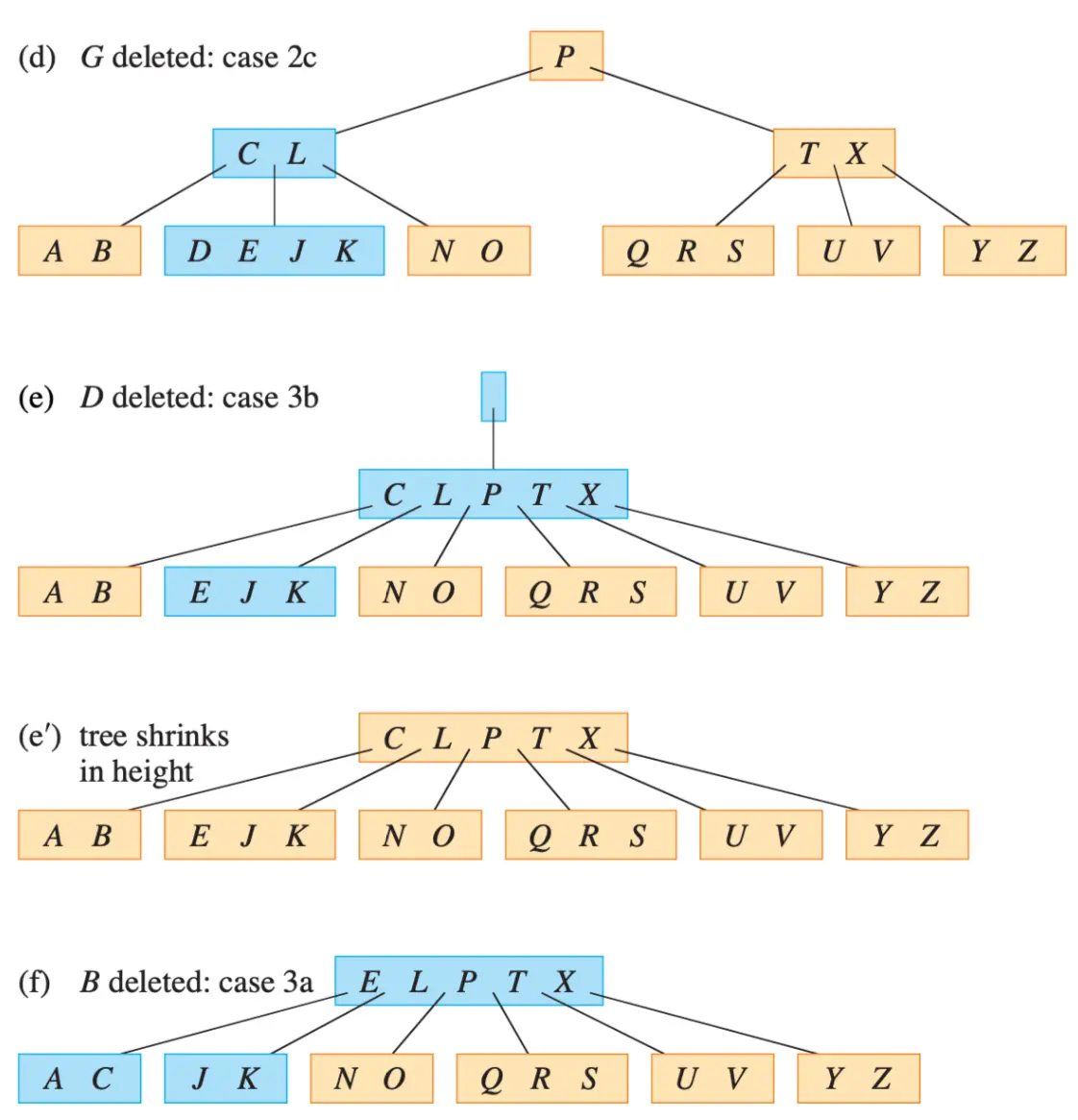
Case 1: Leaf node x, delete x.k if found
Case 2: Internal node x contain k, depending on the number of keys in x.c_i, we have
1. Case 2a: x.c_i has at least t keys. Recursively find the substitute key k' in the subtree rooted at x.c_i and move it up.
2. Case 2b: x.c_i has t - 1 keys and x.c_i+1 has at least t keys. Symmetric to case 2a. Find k' in subtree rooted at x.c_i+1
3. Case 2c: Both x.c_i and x.c_i+1 have t - 1 keys. Merge k and all of x.c_i+1 into x.c_i so that x now have 2t - 1 keys. Then recursively delete k from x.c_i
Case 3: Hold the properties! If x.c_i has only t - 1 keys, execute case 3a or 3b to guarantee descending to a node containing at least t keys.
1. Case 3a: x.c_i has only t - 1 keys but has an immediate sibling with at least t keys. x give a key to x.c_i and sibling give a key to x
2. Case 3b: x.c_i and each(1 or 2) immediate siblings have only t - 1 keys. Merge x.c_i with one sibling and move a key from x down into the newly merged node to become the median key for that node.

t = 3

Fish Touching🐟🎣

Explorer