Knuth Shuffle

It shuffles an array of size $n$ so that $n!$ possible permutations are equiprobable.

Require: array A made of n elements indexed from 0 to n − 1
1: for i = (n − 1)..1 do
2:     j ← random integer in [0, i]
3:     exchange A[i] and A[j]
4: end for

• We count i down because we need a new seed every time we call rand

Proof

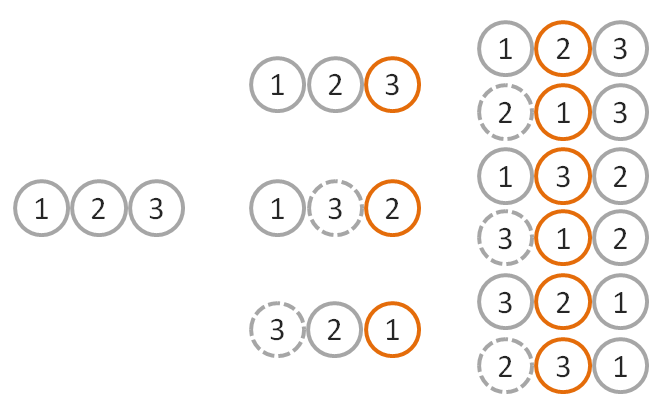
• We start with an array x = [1, 2. ..., N]
  • There are $N!$ possible permutation.
• We consider an arbitrary array x' = [b1, b2, ..., bN], where b1, ..., bN] are distinct integers between 1 and n.
  • Intuition: Every element gets shuffled
  • What’s the Probability that x transferred to x’ ? $\frac{1}{N!}$
  • QED

Optimize?

• The Danger of Naïveté

It’s a nicer? simpler? solution to the shuffling problem:

1. Loop through each card in the deck.
2. Swap the current card with another randomly chosen card.

// CAVET: BIASED
for (int i = 0; i < cards.Length; i++)
{
  int n = rand.Next(cards.Length);
  Swap(ref cards[i], ref cards[n]);
}

The evil lies in rand.Next, where it is always rand.Next(3), giving us $3^3=27$ results. But it should only have $3!$ results. Compared to the original method.

for (int i = cards.Length - 1; i > 0; i--)
{
  int n = rand.Next(i + 1);
  Swap(ref cards[i], ref cards[n]);
}