Prim's Algorithm

What

Used to find a minimum spanning tree. Much like Dijkstra’s algorithm for finding the shortest paths in a graph.
We add only edges that are safe for A. So it qualifies as Greedy since at each step it adds to the tree an edge that contributes the minimum amount possible to the tree’s weight.

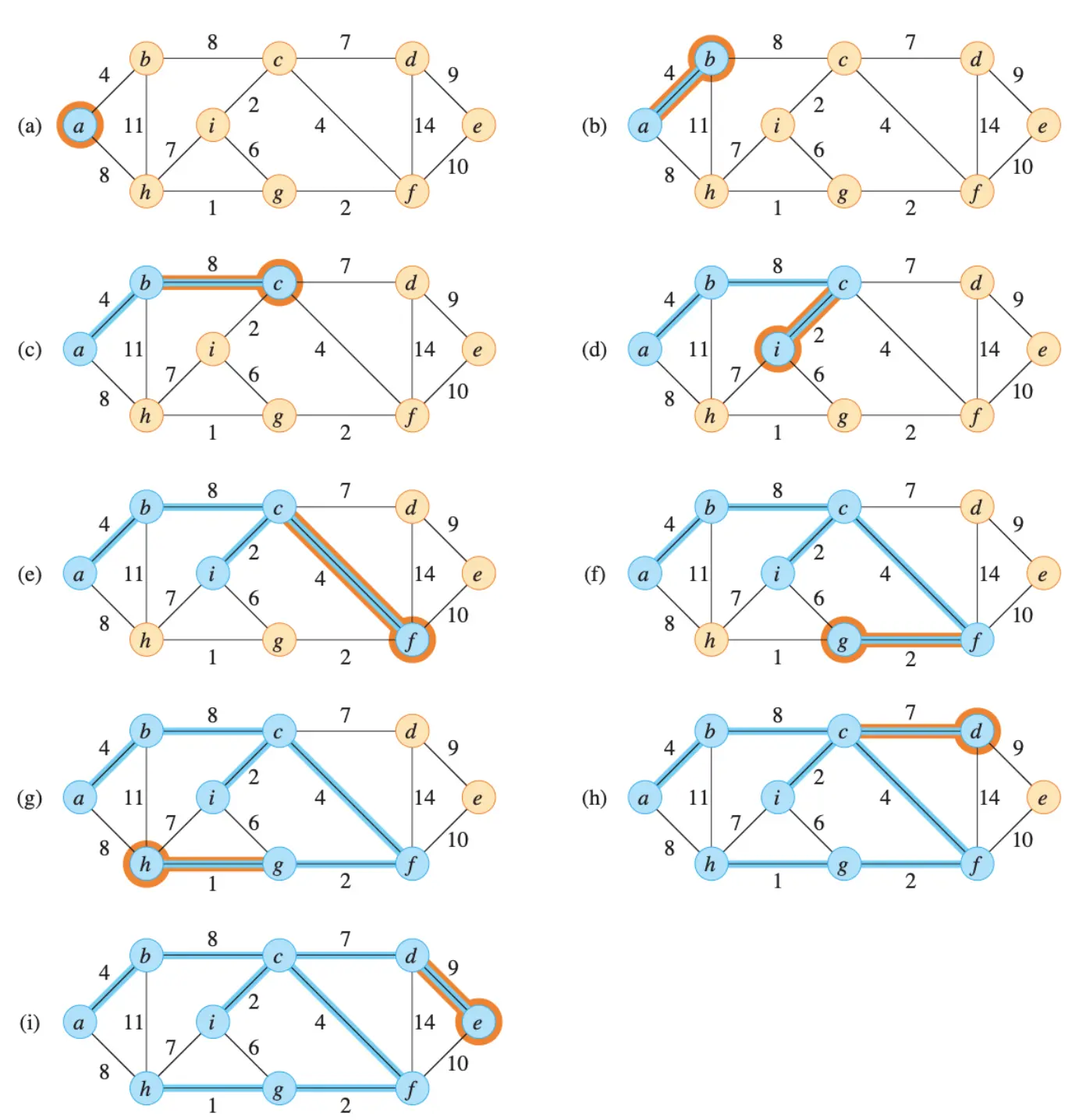
How

The tree starts from an arbitrary root vertex r and grows until it spans all the vertices in V.

1. Pick an arbitrary vertex as starting point, since all vertex must be in the MST, it doesn’t matter which vertex should we start.
2. Push all vertex to a priority queue and set key to infinity except the chosen vertex.
3. Decrease the weight of adjacency vertex to the weight of the edge, can extract the smallest one.
4. Repeat, until there’s no vertex in the queue.

• Running time: $O(E\lg V)$

Why

Prim’s algorithm has the property that the edges in the set A always form a single tree.

Links

Dijkstra’s algorithm